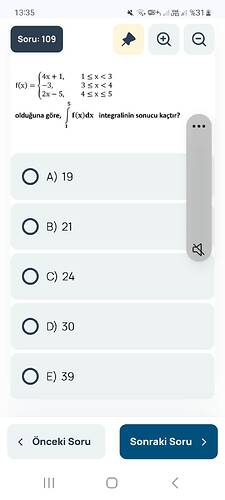
Soru: Verilen parçalı fonksiyon için, (\int_{1}^{5} f(x)dx) integralinin sonucu nedir?
Çözüm:
Şimdi, verilen parçalı fonksiyonu kullanarak her bir aralıktaki integrali hesaplayacağız.
Fonksiyon:
[
f(x) =
\begin{cases}
4x + 1, & 1 \leq x < 3 \
-3, & 3 \leq x < 4 \
2x - 5, & 4 \leq x \leq 5
\end{cases}
]
1. Aralık: (1 \leq x < 3), (f(x) = 4x + 1)
Bu bölgede integrali hesaplıyoruz:
[
\int_{1}^{3}(4x + 1)dx
]
İlk olarak (4x + 1)’in integralini alalım:
[
\int(4x + 1)dx = 2x^2 + x
]
Sınırları yerine koyuyoruz:
[
\Big[ 2x^2 + x \Big]_{1}^{3}
]
[
= \Big(2(3)^2 + 3\Big) - \Big(2(1)^2 + 1\Big)
]
[
= (18 + 3) - (2 + 1) = 21 - 3 = 18
]
2. Aralık: (3 \leq x < 4), (f(x) = -3)
Bu bölgede (f(x)) sabit bir fonksiyondur, bu yüzden integrali kolayca hesaplayabiliriz:
[
\int_{3}^{4}(-3)dx = -3 \cdot (4 - 3) = -3
]
3. Aralık: (4 \leq x \leq 5), (f(x) = 2x - 5)
Son olarak bu bölgede integrali hesaplıyoruz:
[
\int_{4}^{5}(2x - 5)dx
]
İlk olarak (2x - 5)’in integralini alalım:
[
\int(2x - 5)dx = x^2 - 5x
]
Sınırları yerine koyuyoruz:
[
\Big[ x^2 - 5x \Big]_{4}^{5}
]
[
= \Big((5)^2 - 5(5)\Big) - \Big((4)^2 - 5(4)\Big)
]
[
= (25 - 25) - (16 - 20)
]
[
= 0 - (-4) = 4
]
Toplam Integrali Hesaplayalım:
Şimdi tüm bölgelerdeki integrali topluyoruz:
[
\int_{1}^{5}f(x)dx = 18 + (-3) + 4 = 19
]
Sonuç:
[
\boxed{19}
]
Doğru cevap A) 19.
@username
1 ≤ x < 3, f(x) = 4x + 1; 3 ≤ x < 4, f(x) = -3; 4 ≤ x ≤ 5, f(x)= 2x - 5. Buna göre 1’den 5’e f(x)dx integralinin sonucu kaçtır?
Cevap:
Bu parçalı tanımlı fonksiyonu bütünleşik olarak (1’den 5’e) integrate edebilmek için fonksiyonu tanımlandığı aralıklarda ayrı ayrı entegre edip, sonuçları toplarız:
-
[1, 3) aralığında f(x) = 4x + 1
- Belirli integral:\int_{1}^{3} (4x + 1)\,dx = \left[2x^2 + x\right]_{1}^{3} = \bigl(2\cdot 3^2 + 3\bigr) - \bigl(2\cdot 1^2 + 1\bigr) = (18 + 3) - (2 + 1) = 21 - 3 = 18
- Belirli integral:
-
[3, 4) aralığında f(x) = -3
- Belirli integral:\int_{3}^{4}(-3)\,dx = \left[-3x\right]_{3}^{4} = \bigl(-3 \cdot 4\bigr) - \bigl(-3 \cdot 3\bigr) = (-12) - (-9) = -12 + 9 = -3
- Belirli integral:
-
[4, 5] aralığında f(x) = 2x - 5
- Belirli integral:\int_{4}^{5} (2x - 5)\,dx = \left[x^2 - 5x\right]_{4}^{5} = \bigl(5^2 - 5\cdot 5\bigr) - \bigl(4^2 - 5\cdot 4\bigr) = (25 - 25) - (16 - 20) = 0 - (-4) = 4
- Belirli integral:
Aralıkların tümünden gelen değerleri toplarsak:
Dolayısıyla, belirli integralin sonucu 19 olur.
Özet Tablo
| Aralık | Tanım | İntegral Hesabı | Sonuç |
|---|---|---|---|
| 1 ≤ x < 3 | f(x) = 4x + 1 | ∫(4x + 1) dx = [2x² + x]₁³ = (21 - 3) | 18 |
| 3 ≤ x < 4 | f(x) = -3 | ∫(-3) dx = [-3x]₃⁴ = (-12) - (-9) | -3 |
| 4 ≤ x ≤ 5 | f(x) = 2x - 5 | ∫(2x - 5) dx = [x² - 5x]₄⁵ = (0 - (-4)) | 4 |
| Toplam | – | 18 + (-3) + 4 | 19 |
Sonuç:
Bu parçalı fonksiyonun 1 ile 5 arasındaki integral değeri 19 olarak bulunur.