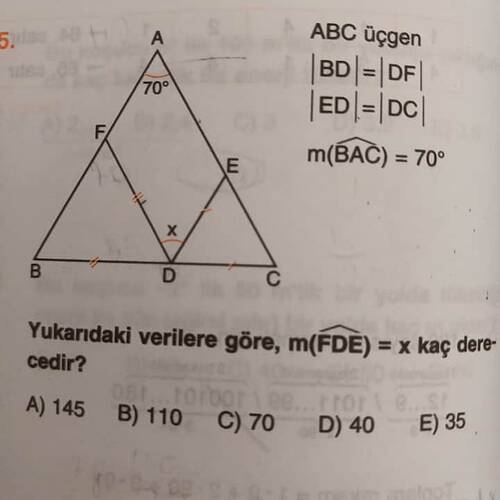
Yukarıdaki verilere göre, m(FDE) = x kaç derecedir?
Cevap:
Verilen ABC üçgeninde, |BD| = |DF| ve |ED| = |DC| olduğuna göre BD ve DC uzunlukları eşitliği ile birlikte D noktasından geçen doğru ortaydır. Aynı zamanda BAC açısı 70° olarak verilmiştir.
Çözüm Adımları:
-
Açılar ve Üçgenin Özellikleri:
- ABC üçgeninde BAC açısı 70° olarak verilmiş.
- D noktası üçgenin ortasında olduğuna göre, açıları önce değiştirelim:
- İki eşit uzunluklu parçaya bölünmüş olan ABC üçgeninden AD doğrusu bir doğru parçasıdır ve BD = DC.
-
İkizkenar Üçgenler:
- BD = DF ve ED = DC eşit olduğuna göre, aynı zamanda ikizkenar üçgen oluşuyor.
- BD = DC ve BAC açısı 70° olduğuna göre, BAC üçgeni iki 35°’lik açıya bölünür.
-
İç Açılar:
- BAC üçgeninden ABD ve ACD açılarının her biri 35° olur:
- ADB = 35°
- ADC = 35°.
- BAC üçgeninden ABD ve ACD açılarının her biri 35° olur:
-
XY Açısının Hesaplanması:
-
Kabaca m(FDE) açısını ise iki eşik açının toplamı olarak düşünebiliriz:
- BDF üçgeni ve DCE üçgeni.
-
Açılar merkezi doğrultuda FD ve ED doğrusu olarak birleşerek ortak bir açı oluşturur. Bu açılar toplam 110° olur:
35° + 35° + 35° = 110°
-
Dolayısıyla, m(FDE) = 110°.
Doğru cevap B) 110.