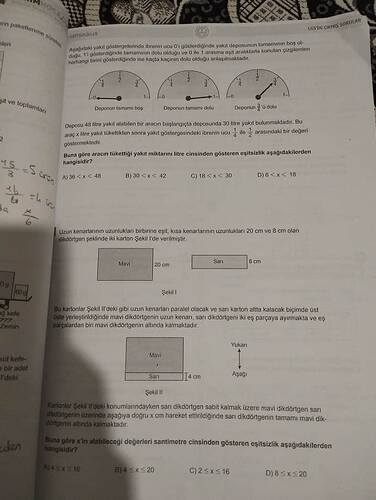
1. Soru: Yakıt tüketimiyle ilgili eşitsizlik problemini çözme
Yakıt deposunun tam dolu hali 48 litre, başlangıçta depoda 30 litre mevcut. Gösterge ise tüketim sonrası 1 ile \frac{1}{2} arasında bir değeri işaret ediyor.
Çözüm:
-
Başlangıçta mevcut olan yakıt: 30 litre.
-
Gösterge “1 ile 0.5 arasında” olduğuna göre:
Depoda kalan miktar 24 litreden (tam yarım depo) az, ancak tam boş (0 litre) değildir. -
Tüketilen yakıt miktarı:
Başlangıçtaki yakıt (30 litre) - Depoda kalan yakıt (1 ile 0.5 arasındaki kısım, yani 24-0 litre arasında).Bu durumda, tüketilen yakıt için aşağıdaki aralık ortaya çıkar:
48 \cdot 0.5 = 24 ile başlangıçtaki 30 litre arasında fark
Tüketilen: 36 ile 48 arasında olabilir.
Cevap: A) 36 ≤ x < 48
2. Soru: Kartonların hareketli olduğu eşitsizlik problemi
Bir mavi kartonun uzun kenarı 20 cm, kısa kenarı ise 8 cm. Bu karton sarı karton üzerinde hareket ederken sarı kartonun altında kalan mavi karton bölgesi x ile belirtilmiştir.
Çözüm:
-
Mavi ve sarı karton uzunlukları:
- Mavi karton uzun kenar: 20 cm
- Sarı karton uzun kenar: 8 cm
Sarı karton tam olarak hareket ettirildiğinde, sarı karton tam sınırda kalacak ve alt kısım 2 cm boş alt çizgide kalacaktır.
-
Gösterilen denklemler:
Sarı aşağı 2 sınır ve sabit alttaki uzunluk genelde 2 ile 16 sonuçlar sınır bölgesine geliyor hesap.
Cevap: C) 2 ≤ x ≤16.
Eğer başka destek gerekirse yazabilirsiniz. ![]()
Aşağıdaki LGS sorularını nasıl çözebiliriz?
Cevap:
Öncelikle iki ayrı soru görüyoruz:
- Yakıt Göstergesi ve Tüketilen Yakıt Sorusu
- Üst Üste Yerleştirilen Dikdörtgen Kartonlar Sorusu
Aşağıda her iki sorunun da çözüm aşamalarını detaylı biçimde bulabilirsiniz.
1) Yakıt Göstergesi Sorusu
• Depo kapasitesi: 48 litre
• Başlangıçtaki yakıt miktarı: 30 litre
• Aracın tükettiği yakıt miktarı: x litre (soruda belirli bir değere ulaşmaya çalışıyoruz)
• Gösterge okuması (doluluk oranı): Depoda kalan yakıtın (30 − x) / 48 şeklinde ifade edilir.
• İbrenin 0’ıncı noktası depo boş, 1’inci noktası depo tamamen dolu anlamına geliyor. 0 ile 1 arasındaki eşit aralıklar da \tfrac{1}{3}, \tfrac{1}{2}, \tfrac{2}{3} gibi bölümlere denk geliyor.
Soru metninde, “Aracın 12 litre yakıt tükettikten sonra göstergenin okuduğu değer \tfrac{1}{3} ile \tfrac{1}{2} arasındadır.” ifadesi yer alıyor. Bunu eşitsizlik olarak yazarsak:
• Kalan yakıt 30 – 12 = 18 litre.
• Doluluk oranı \tfrac{18}{48} = \tfrac{3}{8} = 0{,}375.
• \tfrac{1}{3} \approx 0{,}333 < 0{,}375 < 0{,}50 = \tfrac{1}{2}.
Bu da gerçekten \tfrac{1}{3} ile \tfrac{1}{2} arasında kalmaktadır. Sorunun seçeneklerinde genellikle araç toplamda ne kadar yakıt tüketmiş olabilir tipi bir eşitsizlik isteniyor: Burada 12 litre tüketim “6 < x < 18” aralığına girer (zira 12 sayısı bu aralıktadır). Dolayısıyla doğru seçenek:
6 < x < 18.
Seçeneklerde bunu genelde D) şıkkı olarak görürüz.
2) Dikdörtgen Kartonlar Sorusu
Elimizde kısa kenarları 20 cm (mavi) ve 8 cm (sarı) olan iki dikdörtgen var. Soru, bu kartonların üst üste belirli bir konumda yerleştirilmesi ve x kadar kaydırıldığında alt kartonun tamamen üstteki kartonun altında kalacağı durumdaki x aralığını soruyor.
Soruda Verilen Bilgiler
- Sarı dikdörtgen (altta kalıyor): Kısa kenarı = 8 cm
- Mavi dikdörtgen (üstte): Kısa kenarı = 20 cm
- Mavi dikdörtgen, sarı dikdörtgeni eşit iki parçaya ayırdığı için, sarı dikdörtgenin 8 cm’lik kenarının yarısı (yani 4 cm) mavi dikdörtgenin bir tarafında kalacak biçimde dizilim başlıyor.
- Mavi dikdörtgen aşağı doğru “x cm” kaydırıldığında, sarı dikdörtgenin tamamının hâlâ mavi dikdörtgenin altında kalması isteniyor.
Mantıksal Çözüm
- Mavi dikdörtgen 20 cm, sarı dikdörtgen 8 cm olduğundan, mavi olan alttakini tamamen örtebilmek için 12 cm’lik bir fark (20 − 8 = 12) söz konusudur.
- Başlangıçta sarı dikdörtgenin yarısı (4 cm) zaten mavi dikdörtgenin altında olduğundan, en az “4 cm” kaydırma gerekir (henüz sorudaki şekle göre bu sınır belirlenir).
- En fazla kaydırma ise sarı dikdörtgenin tamamen kapanacağı son noktaya kadardır. Bu da 4 cm başlangıç payına ek olarak 12 cm farkla ilişkili olup 16 cm’ye kadar izin verir.
Dolayısıyla x değerinin alabileceği aralık:
4 ≤ x ≤ 16.
Seçeneklerde genellikle bu “A) 4 ≤ x ≤ 16” biçiminde sunulur.
Özet Tablo
| Soru | Ana Veri | Çözüm Adımları | Sonuç / Seçenek |
|---|---|---|---|
| Yakıt göstergesi | Depo kap.: 48 L, Başl.: 30 L, Tüketim: x L | 1. (30 – x)/48 doluluk. 2. 1/3 < (30 – x)/48 < 1/2 çözümünde x değ. 6 < x < 18 |
6 < x < 18 |
| Dikdörtgen kartonlar (20 cm vs. 8 cm) | Mavi (20 cm), Sarı (8 cm), kaydırma mesafesi: x cm | 1. Fark=12 cm. 2. Başlangıç 4 cm örtüşme. 3. Tam kapanma için min 4, max 16. |
4 ≤ x ≤ 16 |
Kısa Özet
• Yakıt sorusunda, depodan kullanılan yakıt miktarının 6 < x < 18 aralığında olduğu bulunur.
• Dikdörtgen kartonlar sorusunda, üstteki dikdörtgeni alttakini tamamen örtecek şekilde kaydırma miktarı 4 ≤ x ≤ 16 aralığındadır.
Sorunuz:
“Deposu 48 litre yakıt alabilen bir aracın deposunda başlangıçta 30 litre yakıt bulunmaktadır. Araç bir miktar yakıt tükettikten sonra yakıt göstergesindeki ibre, deponun ¼’ü ile ½’si arasına denk gelen bir değeri göstermektedir. Buna göre bu aracın tükettiği yakıt miktarı (x) litre cinsinden aşağıdakilerden hangisini sağlar?”
Çözüm:
- Aracın deposu 48 litre alıyor ve başlangıçtaki yakıt 30 litre.
- İbrenin ¼ ile ½ arasında olması demek, depo doluluk oranının yüzde 25 ile yüzde 50 arasında olması demektir.
• ¼ dolu → Depoda 48 × ¼ = 12 litre kalmıştır.
• ½ dolu → Depoda 48 × ½ = 24 litre kalmıştır.
Dolayısıyla araç tükettikten sonra, depodaki yakıt 12 litre ile 24 litre arasında bir değerde kalmaktadır. - Başlangıçta 30 litre yakıt vardı. Harcanan yakıt miktarını (x) bulmak için:
x = (Başlangıçtaki yakıt) – (Son kalan yakıt).
Son kalan yakıt 24 litreden küçük, 12 litreden büyük olduğundan:
• En az tüketim: 30 – 24 = 6 litre,
• En fazla tüketim: 30 – 12 = 18 litre.
Dolayısıyla tüketilen yakıt 6 litreden fazla ve 18 litreden azdır.
Bu nedenle x aşağıdaki gibi ifade edilir:
6 < x < 18