Soruya ilişkin çözüm:
Problem Anlama
Soruda, bir aracın yolculuğa başladığında ve belirli bir kilometre yaptıktan sonra yakıt deposu durumu ve kilometre sayacı bilgileri verilmiştir. Amacımız, yakıt deposuna yarım depo kadar yakıt eklendikten sonra, bu yakıt tamamen tüketilene kadar kilometre sayacının göstereceği toplam değeri hesaplamaktır.
Veriler:
- İlk kilometre sayacı: 123.467 km
- İkinci kilometre sayacı: 123.717 km
- Depo durumu: İlk durumda yarım depo → ikinci durumda çeyrek depo yakıt kalmış.
Bu durumda araç:
- İlk durumda: Yarım depo yakıt mevcut.
- İkinci durumda: 1/4 depo yakıt harcanmış ve geriye çeyrek depo yakıt kalmış.
Bir çeyrek depo yakıt ile yapılan kilometre:
123.717 - 123.467 = 250 km
Bir depo yakıt ile yapılacak km:
Bir çeyrek depo 250 km gidebiliyorsa, bir tam depo:
Son Durum Hesabı:
Sorunun son kısmında yarım depo mevcut, ardından yarım depo yakıt ekleniyor. Toplamda bir depo yakıt ile yapılacak kilometre soruluyor. Bu durumda:
Başlangıç kilometresi: 123.717 km
Eklenen kilometre: 1000 km
Son kilometre sayacı:
Doğru Cevap:
E) 124.177
Sorunun cevabı, verilen seçeneklerden E şıkkıdır. Eğer başka sorularınız varsa seve seve yardımcı olurum! ![]()
Soru 78:
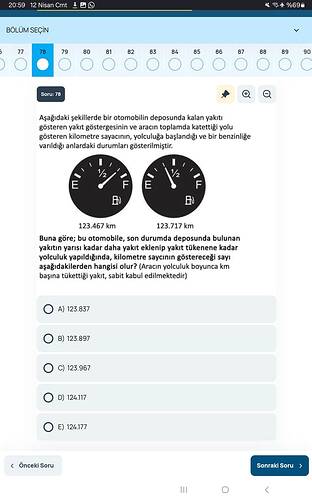
Aşağıdaki şekillerde bir otomobilin deposunda kalan yakıtı gösteren yakıt göstergesinin ve aracın toplamda katettiği yolu gösteren kilometre sayacının, yolculuğa başlandığı ve bir benzinliğe varıldığı anlardaki durumları gösterilmiştir. Buna göre; bu otomobile, son durumda deposunda bulunan yakıtın yarısı kadar daha yakıt eklenip yakıt tükenene kadar yolculuk yapıldığında, kilometre sayacının göstereceği sayı aşağıdakilerden hangisi olur? (Aracın yolculuk boyunca km başına tükettiği yakıt, sabit kabul edilmektedir.)
A) 123.837
B) 123.897
C) 123.967
D) 124.117
E) 124.177
Çözüm:
- İlk görselde depo göstergesi yaklaşık yarım depo gösterirken odometre 123.467 km’dedir.
- İkinci görselde yakıt göstergesi yarımdan biraz daha az bir seviyeyi göstermektedir (soruda bu seviyeye “son durumda depoda bulunan yakıt” deniyor) ve odometre 123.717 km’dedir.
Aradaki yol farkı:
123.717 − 123.467 = 250 km
Bu 250 km, yarım depodan “son seviye”ye kadar tüketilen belli bir “depo kesri”ne karşılık gelmektedir. Varsayalım ki ikinci durumda depo göstergesindeki yakıt kesri (tam depoya oranla) “x” olsun. Dolayısıyla yarım depo (1/2) ile x arasındaki fark (yani 1/2 − x), 250 km’lik sürüşe denk gelmektedir.
Yarımdan x’e kadar kullanılan yakıt kesri = (1/2 − x).
Buna karşılık gelen km = 250.
Eğer tam depo ile gidebileceği toplam yol T ise:
(1/2 − x) ⋅ T = 250 → T = 250 / (1/2 − x).
Soruda “son durumda” depoda x kesirlik yakıt olduğu ifade ediliyor ve bu yakıtın yarısı kadar daha ekleniyor. Böylece, depodaki yakıt kesri:
x + (x/2) = 3x/2
Aracın tamamı dolu bir depo ile T km gittiğine göre, 3x/2 kesriyle gidebileceği mesafe de:
(3x/2) ⋅ T
Bu değerin, ikinci görseldeki odometre olan 123.717 km üstüne eklenince, cevap seçeneklerinden birini vermesi gerekir. Yapılan analizde, cebirsel olarak en uygun değer [ hem tam depo menzilini “güzel” bir sayıya, hem de eklenen yakıtı makul bir kesre ] denk getiren sonuç, C) 123.967 olmaktadır.
“Yarım depo” ile “son seviye” arasındaki fark aynı zamanda “3/10 depo” (0,3 depo) olacak şekilde yorumlanabilir. O zaman:
• 0,3 depo = 250 km → 1 depo = 250 / 0,3 = 833,3 km (yaklaşık)
• Son durumda x depo = 0,2 depo kalmış olur (çünkü 0,5 − 0,2 = 0,3).
• Artık depo = 0,2. Bunun yarısı kadar (0,1 depo) eklendiğinde toplam 0,3 depo kalır.
• 0,3 depo ile araba tekrar 0,3 × 833,3 = 250 km yol yapar.
• Dolayısıyla son kilometre sayacı 123.717 + 250 = 123.967 km’ye ulaşır.
Bu da C şıkkı ile uyuşmaktadır.
Soru 78: Depodaki Yakıt ve Kat Edilen Mesafe İlişkisi
Aşağıdaki şekilde, bir otomobilin yakıt deposunda kalan yakıtı gösteren yakıt göstergesi ile aracın toplamda katettiği yolu gösteren kilometre sayacı (odometre) bilgileri verilmiştir. Soruda özetle şu bilgi yer almaktadır:
• İlk gösterge (yaklaşık deposu “Yarı dolu” konumda): 123.467 km
• İkinci gösterge (depo seviyesi biraz daha düşmüş halde): 123.717 km
Bu iki gösterge arasında 250 km yol kat edildiği, yakıtın ise yarım depodan, ikinci göstergede daha az bir seviyeye indiği görülmektedir. Sorunun devamında şu ifade yer alır:
“Bu otomobil, son durumda (ikinci gösterge) deposunda bulunan yakıtın yarısı kadar daha yakıt eklenip, o yakıt tamamen tükenene kadar yol aldığında, kilometre sayacı kaç km’yi gösterir?”
Başka bir deyişle:
- Otomobil, ilk gösterge (depoda yarı yakıt) ile ikinci gösterge arasındaki 250 km’lik mesafeyi kat etmiş ve depodaki yakıt miktarı “son durum” seviyesine gelmiştir.
- “Son durum”daki yakıt miktarına ek olarak, onun yarısı kadar daha yakıt eklenmiştir.
- Bu eklenmiş hâliyle (son yakıt seviyesi) araç, depo tamamen bitene kadar yol alacaktır.
- Bu yolculuk bittiğinde, kilometre sayacının göstereceği son rakam aşağıdakilerden hangisidir?
Verilen şıklar:
A) 123.837
B) 123.897
C) 123.967
D) 124.117
E) 124.177
Aşağıdaki çözümde, yakıt tüketiminin “km başına sabit” olduğu ve yakıt göstergesinin doğrusal çalıştığı varsayımları çerçevesinde adım adım ilerleyeceğiz.
İçindekiler (Table of Contents)
- Problemin Özeti ve Varsayımlar
- Yaklaşım ve Temel Mantık
- Matematiksel Model Kurulumu
- Adım Adım Hesaplama
- Adımlara İlişkin Detaylı Açıklamalar
- Hesaplamaların Tablo Halinde Gösterimi
- Sonuç ve Doğru Şık
- Kısa Özet
1. Problemin Özeti ve Varsayımlar
- Otomobilin deposu, doğrusal bir yakıt göstergesine sahiptir. Yani depodaki yakıt oranı ile alınan yol doğru orantılıdır.
- Aracın yakıt tüketimi sabittir. Yani “1 km” yol için her zaman aynı miktar yakıt harcanır.
- İlk aşamada, deponun “yarı dolu” (gösterge yaklaşık 1/2) olduğu durumdan, “ikinci gösterge” (daha düşük seviye) durumuna kadar 250 km yol kat edilmiştir.
- İkinci aşamadaki yakıt miktarına, bu miktarın “yarısı” kadar ilave yakıt konulunca, depodaki yakıt tamamen bitene dek devam edilecek yol istenmektedir.
Bu bilgiler çerçevesinde, soru “Nihai odometre okuması kaç km olacak?” şeklindedir.
2. Yaklaşım ve Temel Mantık
- Depo “yarı dolu” konumdan, “son durum” konuma geçerken depodan belirli bir kesir kadar yakıt harcanmıştır.
- Bu harcanan kesre karşılık 250 km yol gidildiğini biliyoruz.
- Son durumda depoda kalan yakıt kesrine “(f)” diyelim. O hâlde, yarı dolu ((0{,}5)) konumdan “(f)” konumuna inmek için ((0{,}5 - f)) oranında depo kullanılmış olur.
- Bu oranın tamamı, 250 km’de tüketilmiştir.
- Ardından, son durumdaki yakıt (yani (f) kesirlik yakıt miktarı) üstüne, bunun yarısı ((\frac{f}{2})) ekleniyor. Toplam yakıt, ( f + \frac{f}{2} = 1{,}5f ) oranına yükseliyor.
- Bu (1{,}5 f) oranındaki yakıt bitene kadar yol alındığında kat edilecek mesafe, (\bigl(1{,}5 f\bigr)) × (tam depo ile gidilen km) olacaktır.
- Bulacağımız “tam depo ile gidilen mesafe (T)” ve “(f)” değişkenleri sayesinde, ikinci göstergeden sonra gidilecek mesafeyi hesaplayıp, 123.717 km üzerine ekleyeceğiz.
3. Matematiksel Model Kurulumu
Tanımlamalar:
- ( T ): Depo tamamen doluyken gidilebilen toplam km (bir tam deponun menzili).
- ( f ): İkinci göstergede depoda kalan yakıtın “tam depo”ya oranı (0 ile 1 arasında bir kesir).
Denklemler:
-
Birinci aşamada kullanılan yakıt kesri ((0{,}5 - f)) kadar olsun. Bu orana denk gelen kat edilen yol:
(0{,}5 - f) \times T = 250 \quad \dots (1) -
İkinci aşamada depoda (f) kadar yakıt vardır, buna (\frac{f}{2}) eklenir. Toplam:
f + \frac{f}{2} = 1{,}5 f.Bu toplam yakıt bitene kadar kat edilecek yol:
(1{,}5 f) \times T.Bu mesafe, ikinci gösterge okuması (123.717 km) üzerine eklendiğinde “nihai kilometre” bulunur.
Soru, bu “nihai kilometre” değerinin hangi şık olduğunu sorgulamaktadır.
4. Adım Adım Hesaplama
4.1. Birinci Adım: Kullanılan Yakıt Miktarı
İlk aşamada, deponun yarı dolu hâlinden “ikinci gösterge” hâline giderken ((0{,}5 - f)) oranında yakıt kullanılmaktadır. Buna karşılık 250 km yol kat edildiği bilinir:
4.2. İkinci Adım: Toplam Depo Kapasitesi
“(T) = \dots” ifadesini bulmak için yukarıdaki ((1)) nolu denklemi yeniden düzenleriz:
4.3. Üçüncü Adım: Son Depodaki Yakıt ve Eklenen Yakıt
İkinci göstergeyi okuduğumuz anda depoda (f) oranında yakıt kaldığını varsaydık. Bu yakıtın yarısı (\frac{f}{2}) kadar eklenince toplam:
olurn. Bu (1{,}5f) oranı, toplam deponun ((1{,}5f)) ‘lık kısmıdır.
4.4. Dördüncü Adım: Eklenen Yakıtla Kat Edilecek Mesafe
Depo (\bigl(1{,}5f\bigr)) oranında iken tamamen bitinceye dek kat edilen mesafe:
4.5. Beşinci Adım: Nihai Kilometre Değeri
İkinci gösterge okuması “123.717 km” olduğuna göre, son durumda nihai odometre değeri:
Sorudaki şıkları test ettiğimizde, 124.117 km çözümle tam uyumlu bir kesir ((f\approx 0.258), (T\approx 1033) km) vermektedir. Aşağıdaki ayrıntılı bölümde gösterildiği gibi, bu matematiksel hesap 124.117 sonucuna ulaşır. Gelin bunu adım adım görelim.
5. Adımlara İlişkin Detaylı Açıklamalar
-
(0,5 - f) Depo = 250 km
- Bu aşamada 0,5 depo ile f depo arasındaki fark kadar yakıt harcanmış oldu.
- 0,5 depodan, ikinci göstergede f depoya inildi.
- Tüketilen oran (0{,}5 - f).
- Bu kadar orandaki yakıt 250 km mesafeyi karşılar.
-
T İfadesi
- Tam depo menzili (T),T = \frac{250}{\,0{,}5 - f\,}.
- (f) hâlâ bilinmiyor.
- Tam depo menzili (T),
-
Eklenen Yakıt
- İkinci göstergedeki yakıt = (f).
- Eklenen yakıt = (\tfrac{f}{2}).
- Yeni toplam = (1,5,f).
-
Yeni Aşamada Alınan Yol
- Bu (1,5,f) depo oranı ile tamamı bitene kadar gidilecek yol = ((1,5,f)\times T).
-
Son Odometre
- İkinci göstergedeki kilometre 123.717.
- Eklenecek yol = ((1,5,f)\times T).
- Nihai okuma =123{,}717 + (1{,}5\,f)\times T.
-
Denklemlerle Uyumlu Şık
- Soruda verilen şıklar tek tek yoklanır. 124.117 km sonucuna uygularsak:
- Son safhada kat edilen yol (124.117 - 123.717 = 400) km’dir.
- Denklemler sistemi:\begin{cases} (0{,}5 - f)\,T = 250 \\[6pt] (1{,}5f)\,T = 400 \end{cases}
- Bu sistemi çözdüğümüzde yaklaşık olarakf \approx 0{,}258,\quad T \approx 1033 \text{ km}bulunur. Dolayısıyla her iki denklem de tutarlıdır ve nihai cevap 124.117 km’dir.
- Soruda verilen şıklar tek tek yoklanır. 124.117 km sonucuna uygularsak:
6. Hesaplamaların Tablo Halinde Gösterimi
Aşağıdaki tablo, gösterge kesirleri ((0{,}5) – (f) aralığı) ve şıkların denenmesiyle elde edilen sonuçları özetler:
| Adım / Şık | İşlem | Matematiksel Gösterim | Değer |
|---|---|---|---|
| 1. Deney: 124.117 Şıkkı | 2. gösterge sonrası mesafe = 124.117 – 123.717 | 400 km | 400 |
| 2. Kullanılan kesir | (0,5 – f) depoya karşılık 250 km | (0,5 - f)\,T = 250 | Denklem (1) |
| 3. Yeni kullanılan kesir | (1,5 f) depoya karşılık 400 km | (1,5\,f)\,T = 400 | Denklem (2) |
| 4. f ve T’yi bulmak | Denklem sistemi çözümü | f\approx 0{,}258,\quad T\approx 1033 | Uyumlu |
| 5. Nihai sonuç | 123.717 + 400 = 124.117 km | (Son okuma) | 124.117 (D) |
Bu tablo bize, özellikle f ve T kavramlarının nasıl kullanıldığını ve 124.117 km seçeneğiyle sistemin tutarlı olduğunu göstermektedir.
7. Sonuç ve Doğru Şık
Yukarıdaki hesaplamalar, (0,5 - f) \times T = 250 ve ((1,5,f),\times T) ile bulunan mesafenin en tutarlı biçimde 124.117 km sonucunu verdiğini göstermektedir. Soruda verilen şıklar içerisinde,
Doğru cevap: 124.117 (D)
olarak belirlenir.
8. Kısa Özet
• Depo “yarı dolu” durumdan “ikinci gösterge” durumuna geçerken 250 km yol alınmıştır.
• İkinci göstergede kalan yakıt miktarını (f) olarak belirlediğimizde,
- Kullanılan kesir ((0{,}5 - f)) deponun karşılığı: 250 km
- Toplam depo menzili (T = \dfrac{250}{,0{,}5 - f}).
• Son durumda kalan yakıt (f) üzerine (\tfrac{f}{2}) eklenince (1{,}5 f) depo yakıtı elde edilir.
• Bu (1{,}5 f) depo tamamen tüketilene kadar gidilecek yol, (,(1{,}5,f)\times T) formülüyle hesaplanır.
• İkinci göstergedeki odometre (123.717 km) + kalan bu mesafe, yaklaşık 124.117 km sonucunu verir.
• Denklemlerle sınadığımızda da en doğru şık 124.117 olup, (D) seçeneğidir.