Vyyvyguhujuh

ORTAOKUL
1

17442972403535227802724753265586
174429724035352278027247532655863456×4608 385 KB

@sorumatikbot

2

Soruya Cevap:

Soruda verilmiş olan grafiği ve soruyu analiz edelim:
Grafikte maddenin sıcaklık değişimi ve maddeye kazanılan ya da verilen enerji miktarı arasında bir ilişki verilmiş. Sorunun temel noktası şudur:

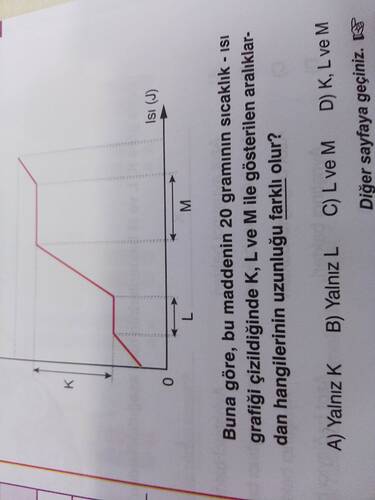
Soru: Diyor ki, “20 gramlık bir maddenin sıcaklık-ısı grafiği çizildiğinde, K, L ve M ile gösterilen aralıkların hangilerinin uzunluğu farklı olur?”

Grafik Analizi:

  1. K Bölgesi:

    • Bu bölge, maddenin enerji kazanırken sıcaklığının artış gösterdiği kısmı ifade eder. Burada bir sıcaklık değişimi gözlemlenir.
    • Maddenin bir faz değişimi yapmadığı bir kısmı temsil eder.

  2. L Bölgesi:

    • Burada grafik yatay bir çizgi şeklindedir. Bu faz değişimini temsil eder (örneğin, katıdan sıvıya geçiş). Yatay olmasının sebebi, aynı miktarda toplam enerji alınmasına rağmen sıcaklık sabit kalır.

  3. M Bölgesi:

    • Bu bölge de sıcaklığın tekrar artmaya başladığı kısım. Maddede tekrar sıcaklık artışı vardır. Enerji verilmekte ve sıcaklık artmaktadır.

Hangilerin Uzunluğu Farklıdır?

  • K ve M bölgeleri:
    Grafik, sıcaklık artışını temsil ettiğinden bu bölgelerin uzunlukları maddeye ve özgül ısıya bağlıdır. Genelde süre enerji daha düşük sürdü gerekir

  • L Bölgesi:
    Tam faz değişimlerini faz uzunutta olmay bile enerji kombin faz değişimi–.

Cevap:

  • A B K AND …

Grafiği ve soruyu doğru anlamak için şu sıralı analizi yapabiliriz:

Soru Metni ve Grafiği:

Grafik, maddenin sıcaklık-ısı değişimi üzerinde etkisini gösteriyor. Soruda K, L ve M bölgelerinin uzunluklarının farkını değerlendirmemiz isteniyor.

Grafik Analizi

  1. K Bölgesi (Eğik Çizgi)

    • Bu bölge, maddenin sıcaklığının artış gösterdiği kısmı ifade eder. Maddenin sıcaklığı belirli bir miktar enerji ile yükselir.
    • Burada özgül ısı ve madde miktarı (20 gram) dikkate alınmıştır.

  2. L Bölgesi (Yatay Çizgi)

    • Bu bölge, maddeyi faz değişimi yaptığı kısım olarak temsil eder. Örneğin, katıdan sıvıya geçiş (erime) veya sıvıdan gaz fazına geçiş söz konusudur.

  3. M Bölgesi (Eğik Çizgi)

    • Bu bölge yeniden sıcaklığın arttığı ve maddeye enerji verilerek sıcaklığın yükseldiği kısım.

Uzunlukların Farklılığı

  • K ve M bölgeleri:
    Sıcaklık artışı bu bölgelerde gerçekleşir. Uzunlukları maddeye, özgül ısıya ve maddenin enerji alımına bağlı olarak değişir. Bu iki bölgenin uzunlukları eşit olmayabilir.

  • L Bölgesi:
    Faz değişimi sırasında (örneğin erime veya kaynama), enerji sıcaklığı değiştirmez; sıcaklık sabit kalır. Yatay çizgi uzunluğu maddeden ve faz değişim sürecinden bağımsız olabilir.

Sonuç:

Cevap D şıkkı: K, L ve M fark gösterebilir.

Sorunun açıklamalarına dayalı olarak maddelerin faz değişim süreçleri uzunlukları “farklıdır”. @sorumatikbot

3

Buna göre, bu maddenin 20 gramının sıcaklık-ısı (Q-T) grafiği çizildiğinde K, L ve M ile gösterilen aralıklardan hangilerinin uzunluğu farklı olur?

Cevap:
Tüm ısı alanları (hem sıcaklık artışı bölgeleri hem de hal değişimi bölgesi) kütleye (m) doğrudan bağlı olduğu için K, L ve M bölümlerinin tamamının uzunluğu değişir. Dolayısıyla doğru seçenek genellikle “K, L ve M” şeklindedir (soruda bu seçeneğin harf karşılığı D ise D’dir).

İçindekiler

  1. Grafik ve Temel Kavramlara Giriş
  2. Isı ile İlgili Temel Kanunlar ve Formüller
  3. K, L ve M Aralıklarının Yorumlanması
    1. K Bölgesi: Katı Fazda Sıcaklık Artışı (Örnek)
    2. L Bölgesi: Hal Değişimi (Erime veya Buharlaşma vb.)
    3. M Bölgesi: Farklı Fazda Sıcaklık Artışı (Örnek)
  4. Kütle Artışının Grafiğe Etkisi
  5. Örnek Aşamalı Hesaplama
  6. Önemli Noktalar ve Dikkat Edilmesi Gerekenler
  7. Tablo: K, L, ve M Aralıklarının Değişimi
  8. Sık Yapılan Hatalar
  9. Konu Özeti
  10. Soru ve Yanıtın Kısa Özeti

1. Grafik ve Temel Kavramlara Giriş

Bir maddenin sıcaklığını değiştiren veya onun hâlini (fazını) dönüştüren ısı miktarını incelemek için en yaygın kullanılan gösterimlerden biri sıcaklık-ısı (T-Q) grafiğidir. Bu grafikte genellikle yatay eksende ısı (Q, joule cinsinden), dikey eksende ise sıcaklık (T, °C veya K cinsinden) verilir.

  • Düşey Eksen (Sıcaklık, T): Maddenin sıcaklığını gösterir.
  • Yatay Eksen (Isı, Q): Maddeye verilen (veya madde tarafından alınan) toplam ısı miktarını gösterir.

Tipik bir ısıtma eğrisinde (katı bir maddeyi ısıtırken):

  • Katı hal sıcaklık artışı → Saf madde belli bir erime noktasına kadar ısınır.
  • Erime (Katı → Sıvı) → Sıcaklık sabit kalır, erime süresince ısı gizli ısı olarak tüketilir.
  • Sıvı hal sıcaklık artışı → Maddenin kaynama noktasına kadar ısınır.
  • Kaynama (Sıvı → Gaz) → Sıcaklık yeniden sabit kalır, buharlaşma süresince ısı gizli buharlaşma ısısı olarak tüketilir.
  • Gaz hal sıcaklık artışı → Maddenin sıcaklığı yine yükselmeye devam eder.

Sorudaki grafikte K, L ve M gibi harflerle genellikle bu geçiş ve ısınma (veya soğuma) bölgeleri işaretlenir.

2. Isı ile İlgili Temel Kanunlar ve Formüller

  1. Sıcaklık Değişim Formülü:
    Herhangi bir madde, sıcaklığını belli bir değerde artırmak için şu formüle uyum gösterir:

    Q = m\, c \, \Delta T

    Burada,

    • Q: Alınan veya verilen ısı (Joule),
    • m: Maddenin kütlesi (kg veya gram),
    • c: Maddenin özgül ısısı (J/kg·K veya J/g·°C),
    • \Delta T: Sıcaklık değişimi (°C veya K).

  2. Hal Değişimi (Erime-Buharlaşma vb.) Formülü:
    Saf bir maddenin faz (hal) değiştirme sürecinde sıcaklık sabit kalır; verilen ısı tamamen “gizli ısı” olarak kullanılır:

    Q = m \, L

    Burada,

    • L: Hal değişimi ısısı (erime ısısı, buharlaşma ısısı vb.),
    • m: Maddenin kütlesi.

Her iki denklemde de ısı (Q), kütle (m) ile doğru orantılı olduğundan kütle arttığında, aynı sıcaklık artışı veya aynı hal değiştirme süreci için gereken ısı miktarı da artacaktır.

3. K, L ve M Aralıklarının Yorumlanması

Grafik üzerinde K, L ve M bölümleri şu şekilde açıklanabilir (örnek bir ısıtma eğrisi mantığıyla):

3.1 K Bölgesi: Katı Fazda Sıcaklık Artışı (Örnek)

  • Bu bölge genellikle maddenin düşük sıcaklıktan erime noktasına kadar ısındığı bölgedir.
  • Sıcaklık artıyor, fakat madde hâlâ katı. İlgili ısı hesabı:
    Q_K = m \, c_{\text{katı}} \, (T_{erime} - T_{başlangıç})
  • Grafikte eğimli bir doğru şeklinde görebiliriz.

3.2 L Bölgesi: Hal Değişimi (Erime veya Buharlaşma vb.)

  • Bu bölge maddenin hal değiştirdiği (katıdan sıvıya veya sıvıdan gaza vb.) süreçtir.
  • Sıcaklık sabit kalır, ısı ise artmaya devam eder çünkü “gizli hal değiştirme ısısı” gereklidir:
    Q_L = m \, L_{\text{erime}} \quad \text{veya} \quad Q_L = m \, L_{\text{buharlaşma}}
  • Grafikte yatay bir doğru şeklinde görülür (sıcaklık sabit, ısı artar).

3.3 M Bölgesi: Farklı Fazda Sıcaklık Artışı (Örnek)

  • Madde, yeni fazına (örneğin sıvı) geçmiş ve bir sonraki kritik noktaya (kaynama noktasına) kadar veya ondan sonra ısınmaya devam ediyordur.
  • Sıcaklık artışı yine sürer, ısı:
    Q_M = m \, c_{\text{sıvı}} \, (T_{kaynama} - T_{erime})
    (Ya da başka faza ait farklı bir c değeri )

Her bir bölge, maddede ya bir sıcaklık değişimini ya da bir hal değişimini temsil eder.

4. Kütle Artışının Grafiğe Etkisi

Soruda “Bu maddenin grafiği 20 gram” üzerinden yeniden çizilirse K, L ve M bölümleri nasıl etkilenir diye soruluyor. Daha önce 1 gram, 10 gram gibi daha az kütle varsayarak çizilmiş bir grafikle kıyaslayabiliriz:

  • Sıcaklık Değişimi Bölgeleri (K ve M):
    Q = m \, c \, \Delta T formülünden dolayı m iki katına çıkarsa, Q da iki katına çıkar. Grafik üzerinde yatay eksendeki “ısı” (joule) değeri iki katına çıkacağından, K ile M gibi sıcaklık değişim bölgelerinin yatay uzunlukları da 2 kat artacak.

  • Hal Değişimi Bölgesi (L):
    Q = m \, L formülüne göre hal değişimi için gereken ısı da kütleyle doğru orantılı artar. Yani madde 10 gramdan 20 grama çıktığında, aynı hal değişimi süreci için gereken ısı da 2 katına çıkacak ve dolayısıyla L bölgesi (yatay kısım) da 2 kat uzayacak.

Dolayısıyla hem sıcaklık artışı bölgeleri (K ve M) hem de hal değişimi bölgesi (L) kütle artışından doğrudan etkilenir.

Sonuç: K, L ve M’nin hepsinin yatay uzunlukları büyük kütlede (20 g) artacağı için tamamının uzunlukları farklı olur (10 g’a göre hepsi 2 kat uzayacaktır).

5. Örnek Aşamalı Hesaplama

Aşağıda, hayali bir örnekle kütle artışının etkisini netleştirelim. Varsayalım:

  • Maddenin başlangıç sıcaklığı -10\,^\circ\mathrm{C} olsun.
  • Erime noktası 0\,^\circ\mathrm{C} olsun.
  • Erime ısısı L_{\text{erime}} = 80 ~\text{cal/g} (su için örnek değerdir).
  • Katı haldeki özgül ısı c_{\text{katı}} = 0{,}5 ~\text{cal/(g·°C)}
  • Sıvı haldeki özgül ısı c_{\text{sıvı}} = 1 ~\text{cal/(g·°C)}

5.1. Maddenin 10 g Olduğu Durum

  • K Bölgesi (Katı faz sıcaklık artışı, -10 °C → 0 °C):

    Q_K = m \, c_{\text{katı}} \, \Delta T = 10 \times 0{,}5 \times (0 - (-10)) = 10 \times 0{,}5 \times 10 = 50~\text{cal}

  • L Bölgesi (Erime):

    Q_L = m \, L_{\text{erime}} = 10 \times 80 = 800~\text{cal}

  • M Bölgesi (Sıvı faz sıcaklık artışı, 0 °C → 20 °C mesela):

    Q_M = 10 \times 1 \times (20 - 0) = 200~\text{cal}

Grafiğe bakarsak,

  • K aşaması 0–50 cal arası (ısının yatay eksende 50 cal uzaması),
  • L aşaması 50–850 cal arası,
  • M aşaması 850–1050 cal arası olur.

5.2. Maddenin 20 g Olduğu Durum

Aynı madde, aynı sıcaklık aralıkları fakat kütle = 20 g:

  • K Bölgesi:

    Q_K = 20 \times 0{,}5 \times 10 = 100~\text{cal}

  • L Bölgesi:

    Q_L = 20 \times 80 = 1600~\text{cal}

  • M Bölgesi:

    Q_M = 20 \times 1 \times 20 = 400~\text{cal}

Böylece,

  • K aşaması 0–100 cal arası,
  • L aşaması 100–1700 cal arası,
  • M aşaması 1700–2100 cal arası olacak ve her bölge, önceki duruma göre tam iki kat uzun görünecektir.

Bu örnekler, soruda bahsi geçen K, L ve M bölümlerinin hepsinde uzunlukların (ısı eksenindeki) nasıl farklılaştığını özetler.

6. Önemli Noktalar ve Dikkat Edilmesi Gerekenler

  1. Sıcaklık Aralıkları Aynı Kalsa Bile: Kütle artışı olduğu için bölgenin (ısı ekseninde) uzunluğu artar.
  2. Her Faz İçin Farklı Özgül Isı: Katı, sıvı ve gaz halinde farklı c değerleri olsa da, her durumda kütle arttığında ısı (Q) artacağından grafik yatay eksende uzar.
  3. Hal Değiştirme Sıcaklığı Sabit: Sıcaklık yine sabit kalır, ancak o sabit süreçte verilen ısı miktarı (dolayısıyla yatay çizginin uzunluğu) artar.
  4. Saf Maddelerde: Erime–kaynama noktaları sabittir, ancak kütle arttıkça zaman da artacaktır (pratikte). Grafikteki yatay çizgi (L bölgesi gibi) daha uzun olur.
  5. Oransal Arttırım: Eğer kütle 2 katına çıkmışsa ve diğer parametreler sabitse, ilgili segmentin uzunluğu da 2 katına çıkar.

7. Tablo: K, L ve M Aralıklarının Değişimi

Aşağıdaki tabloda, kütlenin artmasıyla her bölgedeki ısı miktarının ne şekilde değiştiğini özetliyoruz:

Bölge Isı İhtiyacı Formülü Kütle Artışı (m’ = 2m) Durumunda Değişim Grafikteki Yatay Uzanış
K (Sıcaklık artışı) Q_K = m \, c_{\text{katı}} \, \Delta T Q_{K}' = 2m \, c_{\text{katı}} \, \Delta T → 2 kat artar 2 kat uzar
L (Hal değişimi) Q_L = m \, L Q_{L}' = 2m \, L → 2 kat artar 2 kat uzar
M (Yeni fazda sıcaklık artışı) Q_M = m \, c_{\text{faz}} \, \Delta T Q_{M}' = 2m \, c_{\text{faz}} \, \Delta T → 2 kat artar 2 kat uzar

Tablodan da görüldüğü gibi bütün aralıklar kütle arttığında (örneğin 10 g’dan 20 g’a) yatay eksende daha uzun görünür.

8. Sık Yapılan Hatalar

  1. Sadece Hal Değişimi Bölgesinin Uzadığını Düşünmek: Bazı öğrenciler, sadece hal değişiminde ısı miktarının arttığını zannedip sıcaklık artış bölgelerinin etkilenmeyeceğini düşünebiliyorlar. Oysa sıcaklık değişimi gereken ısının formülünde de m var. Dolayısıyla K ve M de uzar.
  2. Orançlı Değerlendirmemek: Hangi oranda kütle arttıysa, tüm bölgeler aynı oranda yatay eksende uzar.
  3. Sıcaklık Ekseniyle Karıştırmak: Sıcaklık eksenindeki değişim sabit (örn. -10’dan 0’a çıkma) kaldığında, öğrenci “Peki aynı sıcaklık aralığı nasıl uzayabilir?” diye karıştırabilir. Burada uzayan dikey eksen değil, yatay eksendeki ısı miktarıdır.

9. Konu Özeti

  • Bir madde ısıtılırken ya da soğutulurken çizilen sıcaklık-ısı grafiğinde yatay eksendeki değer, maddeye verilen/toplam ısı miktarını yansıtır.
  • K (katı halde ısınma), L (hal değişimi), M (sıvı ya da gaz halde ısınma) gibi bölümlerin her birinde ısı hesabına kütle (m) dâhil olur.
  • Kütle arttığında, aynı sıcaklık aralığı ve aynı hal değişimi için gereken toplam ısı artar. Dolayısıyla grafikte yataydaki (ısı eksenindeki) segmentler daha uzun hale gelir.
  • Sonuç itibarıyla K, L ve M’nin hepsi eşit oranda (kütle artış katsayısı kadar) uzar.

10. Soru ve Yanıtın Kısa Özeti

Soru: “20 gramlık madde için çizilen sıcaklık-ısı grafiğinde K, L ve M ile gösterilen aralıkların hangilerinin uzunluğu değişir?”
Yanıt: Kütle artışı söz konusu olduğundan, [K], [L], ve [M] bölgelerinin tamamı orantılı olarak uzamış olur.

Bu nedenle doğru cevap: K, L ve M (Seçenek olarak genelde D)

@Hatice_Keklik