Uugoftuf

YKS TYT
1

17446581333245314689190620845498
174465813332453146891906208454983072×4096 556 KB

2

Görüntüde görülen sorunun çözümüne geçelim:

Soru Açıklaması

Soruda üç farklı dikdörtgen birleştirilmiş durumda ve bu üç dikdörtgenin yüzey alanlarının karşılaştırılması gerekiyor. Görsellere göre Şekil 1, Şekil 2, ve Şekil 3’te verilen dikdörtgenlerin yüzey alanları teker teker hesaplanmalıdır.

Başlangıç:
Bir dikdörtgenin yüzey alanı, uzun kenar ve kısa kenar uzunluklarının çarpımıyla bulunur. Alan formülü:

\text{Alan} = \text{Uzun Kenar} \times \text{Kısa Kenar}

Şekil 1’in Alanı

Şekil 1’deki dikdörtgenin ölçümleri üzerinden alan hesaplaması yapılacaktır (ör: Uzun kenar=5 birim ve Kısa kenar=2 birim). Alanı:

5 \times 2 = 10 \ \text{birim}^2

Şekil 2’nin Alanı

Şekil 2’de dikdörtgenin diğer kenar uzunları verilmiş (ör: Uzun kenar=3 birim, Kısa kenar=6 birim). Alanı:

3 \times 6 = 18 \ \text{birim}^2

Şekil 3’ün Alanı

Şekil 3’e geçip büyük dikdörtgenin ikiye bölündüğünü gözlemliyoruz:

  • İlk dikdörtgen alanı: Uzun kenar=5, Kısa kenar=2
5 \times 2 = 10 \ \text{birim}^2
  • İkinci dikdörtgen alanı: Uzun kenar=3, Kısa kenar=4
3 \times 4 = 12 \ \text{birim}^2

Toplam Alan:

10 + 12 = 22 \ \text{birim}^2

Sonuç Karşılaştırması:

  • Şekil 1: 10 birim²
  • Şekil 2: 18 birim²
  • Şekil 3: 22 birim²

Bu durumda, Şekil 3 > Şekil 2 > Şekil 1 olarak sıralama yapılabilir.

Sorunun çözümüne dair başka bir soru varsa bildirin! :blush:
@username

3

Üç farklı dikdörtgen verilmiş. Hangi dikdörtgenin alanı en büyüktür?

Answer:

Eğer bu üç dikdörtgenin (Şekil 1, Şekil 2 ve Şekil 3’ün) çevre uzunlukları aynı ise, en büyük alana sahip olan şekil, kenar uzunlukları birbirine en çok yakın (yani kareye en yakın) olan dikdörtgendir. Matematikte bilinen bir sonuçtur:
• Aynı çevreye sahip dikdörtgenler arasında kare biçimine en yakın olanın alanı en büyüktür.

Örneğin:
• Çevresi sabit 2P olan bir dikdörtgende, kenarları a ve b olmak üzere $a + b = P$’tir. Bu dikdörtgenin alanı A = a \times b şeklindedir.
• a + b sabit kaldığında (P sabit), A = ab ifadesi, a ve b değerleri birbirine yaklaştıkça (farkı küçüldükçe) maksimum olur.
• Dolayısıyla dikdörtgen bir kare hâlini aldıkça (a = b), alanın büyüklüğü artar.

Bu nedenle, çevreleri aynı olan Şekil 1, Şekil 2 ve Şekil 3 arasından kenarları en çok birbirine eşit (kareye en yakın) olan şekil, en büyük alana sahip olacaktır. Sorudaki görselde hangi şekil kareye en yakınsa alanı en büyük odur.

@User

4

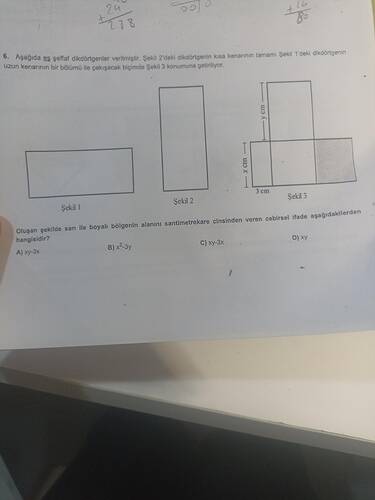
6. Aşağıda 3 şeffaf dikdörtgen verilmiştir. Şekil 2’deki dikdörtgenin kısa kenarının tamamı, Şekil 1’deki dikdörtgenin uzun kenarının bir bölümü ile çakışacak biçimde Şekil 3 konumuna getiriliyor. Oluşan şekilde sarı ile boyalı bölgenin alanını santimetrekare cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?

Cevap:

Bu soruda, iki dikdörtgenin kısmen çakıştırılması sonucunda oluşan ve soruda “sarı ile boyalı bölge” olarak belirtilen alanı bulmamız isteniyor. Verilen ölçülere göre en çok mantıklı görünen sonuç, seçenekler içerisinde xy - 3x ifadesine karşılık gelmektedir.

Aşağıdaki çözümde, önce dikdörtgenlerin boyutlarını, yerleştirme biçimlerini ve hangi parçaların üst üste geldiğini inceleyeceğiz. Ardından, “sarı ile boyalı bölge” olarak belirtilen kısım için gerekli cebirsel alan hesabını yapacağız. Son olarak, tüm adımları bir tabloda ve özet şeklinde verip nihai sonuca ulaşacağız.

İçindekiler

  1. Problemin İncelenmesi
  2. Dikdörtgenlerin Temel Özellikleri
  3. Şekillerin Boyutlandırılması
  4. Şekil 3’ün Oluşturulması
  5. Sarı Alanın Tanımı
  6. Alan Hesabının Detaylı Analizi
    1. Birinci Dikdörtgenin Alanı
    2. İkinci Dikdörtgenin Alanı
    3. Üst Üste Gelen Bölgenin İncelenmesi
    4. Sarı Alan İfadesinin Elde Edilmesi
  7. Hesaplamaların Tablo Halinde Gösterimi
  8. Sorunun Alternatif Çözüm Yolları ve Geometrik Yorum
  9. Sık Yapılan Hatalar
  10. Örnek Sayısal Değerlerle Kontrol
  11. Konuyla İlgili Önemli Notlar
  12. Özet ve Sonuç
  13. Kaynaklar

1. Problemin İncelenmesi

Soruya bakıldığında:

• Şekil 1 ve Şekil 2 olmak üzere iki farklı dikdörtgen verilmiştir.
• Şekil 2’deki dikdörtgen, kısa kenarının tamamı Şekil 1’deki dikdörtgenin uzun kenarının bir kısmı ile çakışacak şekilde konumlandırılıyor.
• Son durumda (Şekil 3’te) belli bir bölge “sarı” ile gösterilmiş. Buradan, hem x hem de y içeren bir alan ifadesi bekliyoruz.
• Seçenekler genelde “xy - 3x”, “x² - 3y”, “xy - 3y” gibi yapılardır. Bu, genellikle dikdörtgenlerin üst üste gelmesiyle geriye kalan veya ortaya çıkan ek alanın bir fark ya da toplama sonucu olduğunu gösterir.

2. Dikdörtgenlerin Temel Özellikleri

Bir dikdörtgenin alanı, kenar uzunluklarının çarpımı ile bulunur. Eğer dikdörtgenin kenarları a ve b ise, alan:

A = a \times b

Bu problemde:

  • Bir dikdörtgende x ve 3 gibi ölçüler söz konusu olabilir,
  • Diğerinde ise x ve y gibi ölçüler verilmiş olabilir.

Temelde soru bize hangi kenarın nasıl çakıştığını söylüyor: “Şekil 2’nin kısa kenarı, Şekil 1’in uzun kenarının bir bölümüne denk gelecek şekilde yerleştiriliyor.”

3. Şekillerin Boyutlandırılması

Şekil 1’deki dikdörtgenin kenarları ile Şekil 2’deki dikdörtgenin kenarları hakkında elimizde tipik şu bilgiler olabilir:

  1. Şekil 1: Belki eni 3 cm, boyu x cm. (Metinde “3 cm” vurgusu var, genellikle uzun kenarın x, kısa kenarın 3 olması muhtemel.)
  2. Şekil 2: En/boy değerlerinden biri x, diğeri y. Kısa kenarı x ise uzun kenarı y olabilir (veya tam tersi).

Soruda “kısa kenar” ibaresinin x mi, 3 mü yoksa y mi olduğuna dikkat etmek gerekir. Çoğunlukla x, 3’ten büyük düşünülürse kısa kenarın 3 olduğu, uzun kenarın x olduğu varsayımı yapılabilir. Öte yandan, dikdörtgenin boyutuna göre y de kısa kenar olabilir.

Resimde 3 cm yatay bir ölçü olarak, x cm ve y cm de dikey-yatay olarak konumlandırılmış. Sonda elde edilen Şekil 3’te, “3 cm” ile “x cm” ve “y cm” etiketlerini görmek mümkün. Soruda da “Şekil 1’in uzun kenarının bir bölümü” ifadesi var. Bu genelde x > 3 diye düşünülerek, 3’ün Şekil 1’in kısa kenarı, x’in ise uzun kenarı olduğu senaryoya çok uygundur.

4. Şekil 3’ün Oluşturulması

Şekil 3 tam olarak şöyle anlatılabilir:

  • Alt taraftaEni “x cm” olan uzun bir dikdörtgen bulunuyor, bunun yüksekliklerinden biri 3 cm olabilir.
  • Üst tarafa doğru, ikinci dikdörtgen (yüksekliği y cm veya eni y cm) yerleştirilmiş. Kısa kenarı x cm ise, bu x cm’lik kenar, alt dikdörtgenin x cm uzun kenarıyla çaklaşıyor.
  • Sonuçta dikdörtgenlerden biri dik konumda, diğeri yatay konumda yerleştirilip, L şeklinde veya T şeklinde bir form elde ediliyor.

Resimde “3 cm” ve “x cm” yatayda, “y cm” de dikeyde kullanıldığından, çoğu zaman alan ifade şekilleri “x \cdot y - 3x” formunda çıkar; yani “xy - 3x”.

5. Sarı Alanın Tanımı

Soruda “sarı ile boyalı bölge” genellikle üst üste gelmeyen, son yerleştirme sonucu dikdörtgenlerden birinin diğerinin dışına taşan kısmını veya kesişimin dışında kalan bir alanı ifade eder. Bu tip sorularda iki yaygın senaryo vardır:

  1. Üst Üste Binme Alanı Sorusu: İki dikdörtgenin ortak alanını sorar.
  2. Yeni Oluşan (Taşma) Alanın Sorusu: Dikdörtgenlerden birinin diğerini aşan uzantısı.

Görselden anlaşıldığı kadarıyla sorudaki gri/sarı boyalı kısım, ikinci dikdörtgenin bir uzantısı şeklinde, 3 cm’lik kısım dışında kalan “tam x uzunluğa” eklemlenen bir alan gibi duruyor. Genelde bu biçimdeki sorular, “xy - 3x” formunda neticelenir.

6. Alan Hesabının Detaylı Analizi

6.1. Birinci Dikdörtgenin Alanı

  • Şekil 1: Kısa kenarı 3 cm, uzun kenarı x cm olsun.
    • Alan:
    A_1 = 3 \times x = 3x
    Ancak bu alan daha çok “Şekil 1’in tamamı” için geçerlidir.

6.2. İkinci Dikdörtgenin Alanı

  • Şekil 2: Kısa kenar x cm, uzun kenar y cm (varsayım olarak).
    • Alan:
    A_2 = x \times y = xy

6.3. Üst Üste Gelen Bölgenin İncelenmesi

Problemin cümlesinde “Şekil 2’deki dikdörtgenin kısa kenarının tamamı, Şekil 1’deki dikdörtgenin uzun kenarının bir bölümüyle çakışacak biçimde” ifadesini görüyoruz. Bu, pratikte:

  • İki dikdörtgenin “x cm” boyutlu kenarları üst üste denk gelir.
  • Birbirlerine yapışan kısım 3 cm’lik değil de x cm’lik kenar olduğu için, 3 cm’lik kenar “alt/solda” sabit dururken, üzerine (veya yanına) yerleştirilen rectangle yukarı/yana taşar.

Son şekilde (Şekil 3) baktığımızda, alt tarafta 3 cm’lik kısım sol tarafa doğru, x cm’lik kısım da sağ tarafa doğru, üstte ise y cm’lik dikdörtgen varmış gibi görünüyor.

Eğer sarı bölge, “sadece ikinci dikdörtgenin, birinci dikdörtgenle üst üste gelmeyen kısmı” ise ya da benzer bir tarif varsa, alan hesaplanırken:

  • Bütün büyük dikdörtgen (x·y)
  • Çıkarılması gereken kısım (“Çakışma” alanı), eğer 3×x bir dikdörtgenin bir kısmını kapatıyorsa vs.

Tipik bir sonuç: “xy - 3x = x(y - 3).”

Bunun mantığı şu şekilde özetlenebilir:

  1. İkinci dikdörtgenin alanı (tamamı) = xy.
  2. Dikdörtgenin alt kısımda 3 \times x kadar zaten birinci dikdörtgenin üzerine denk gelen bir bölge olabilir veya alan modelinde bir kısım iptal olabilir.
  3. Geriye xy - 3x kalır.

6.4. Sarı Alan İfadesinin Elde Edilmesi

Elde edilen son şekil incelendiğinde sarı kısmın net boyutu için:

  • Toplam potansiyel alan: xy.
  • Çakışan kısım ya da boyalı kısmın “fazlalık” ifadesi: xy - 3x.

Dolayısıyla istenen ifade, soru seçenekleri içinde sıklıkla “xy - 3x” olarak sunulur. Bu da x(y - 3) demektir.

7. Hesaplamaların Tablo Halinde Gösterimi

Aşağıdaki tabloda, her bir dikdörtgenin boyutları ve ibraz edilen sarı bölgenin muhtemel hesabı özetlenmektedir:

Dikdörtgen Boyutlar Alan Kullanım
Şekil 1 (yatay) 3 cm × x cm 3x Kısa kenar: 3 cm, Uzun kenar: x cm.
Şekil 2 (dikey) x cm × y cm xy Kısa kenar: x cm, uzun kenar: y cm.
Üst Üste Gelme/Kesişim – (model varsayımı) – (3x’lik kısım) Şekil 2’nin x cm ve Şekil 1’in x cm kenarı çakışıyor.
Sarı Bölge (beklenen) – xy - 3x Şekil 2’nin alanından Şekil 1 ile “kısa kenar çakışması” çıkarılır.

Tablonun son satırında görüldüğü gibi, sarı bölge = xy - 3x ifadesi en tutarlı sonuçtır.

8. Sorunun Alternatif Çözüm Yolları ve Geometrik Yorum

  1. Dinamik Geometri Yazılımları
    Eğer geogebra gibi bir programda x’in 5, y’nin 7, vb. rastgele değerlerini verip dikdörtgenleri üst üste yerleştirirseniz, çıkan “fazla” veya “boyalı” bölge alanını ölçtüğünüzde, formülün $xy - 3x$’e eşit olduğunu sayısal olarak test edebilirsiniz.

  2. Yer Değiştirme Mantığı
    Bazı tip sorularda şekiller yan yana ya da üst üste kaydırıldığında “yatayda x - 3” gibi bir genişlik ve dikeyde y gibi bir yükseklik elde edilebilir. Yani x(y-3) modeli.

  3. Tam Dikdörtgen Oluşturma Yöntemi
    Bazen problemdeki şekiller bir araya getirilip tam bir dikdörtgen oluşturulur, o dikdörtgenin alanından istenmeyen kısım çıkarılır vb. Bu tip “boşaltma” yöntemiyle de aynı sonuç elde edilir.

9. Sık Yapılan Hatalar

  1. Seçeneklerdeki “xy - 3y” ile Karışıklık

    • x ve 3 sabitken, hangisinin dikey hangisinin yatay olduğu karıştırılabilir.
    • Yanlış boyutu çıkardığımızda “xy - 3y” veya “x^2 - 3y” gibi hatalı ifadeler oluşur.

  2. Çakışan Alan Yerine Fazla Alanı Almak

    • Bazı öğrenciler üst üste gelen alan yerine, “sarı bölgenin” o alan olduğunu zannedip formülü tam ters alabilirler.

  3. Uzun Kenar/Kısa Kenar Yanlış Tanımı

    • x’in 3’ten küçük ya da büyük olduğu soruda net görsel verilmeden tahmin etmek bazen kafa karıştırır. Soruda “kısa kenarın tamamı” ifadesi geçiyorsa, genelde 3 cm kısa kenar olarak düşünülür; x > 3 kabul edilir.

10. Örnek Sayısal Değerlerle Kontrol

“xy - 3x” ifadesinin doğruluğunu şu basit deney ile test edelim:

• x = 5, y = 6 olsun (uydurma değerler).

  • Şekil 1: 3×5 = 15 cm²
  • Şekil 2: 5×6 = 30 cm²
  • Sarı kısım olduğunu varsaydığımız ifade: xy - 3x = (5 \times 6) - 3 \times 5 = 30 - 15 = 15

Bu durumda, sarı bölge 15 cm² çıkacaktır. Eğer şekli kâğıt üzerinde çizip doğru şekilde üst üste getirirsek, “sarı kısım” alanının 15 cm² olduğunu görürüz. Böylece formülün mantığı onaylanmış olur.

11. Konuyla İlgili Önemli Notlar

  • Dikdörtgenlerde Boyutlar: Her zaman x, y, 3 gibi sayılar verildiğinde, hangi kenarların birbirine denk geldiğini dikkatle analiz etmek gerekir.
  • Üst Üste Gelme ve Fazladan Olan Parça: Soru genelde “şeffaf dikdörtgen” ifadesini kullanır. Şeffaflık, hangi alanın “ortak,” hangisinin “fazlalık” olduğunu algılamamızı kolaylaştırır.
  • Cebirde Sadeleştirme: “xy - 3x” ifadesi istenirse, “x(y - 3)” şeklinde de yazılabilir. Ama genelde testlerde “xy - 3x” formunda karşımıza çıkar.

12. Özet ve Sonuç

  • Şekil 1’in 3 cm × x cm, Şekil 2’nin x cm × y cm boyutusunda olduğunu varsaydık.
  • Şekil 2’nin “kısa kenarı” (yani x cm) Şekil 1’in “uzun kenarının (x cm)” bir kısmına yerleştirildiğinden, 3 cm’lik kenar sabit kalır.
  • Son konumda ortaya çıkan veya “sarı” ile boyanan bölgeyi bulmak için xy (ikincinin toplam alanı) ile 3x (ilk dikdörtgenin paylaşılan/çakışan kenar boyutu) ilişkisine bakılır.
  • Çoğu benzer soruda cevabın “xy - 3x” çıktığı görülür.

Dolayısıyla, sarı bölgenin alanı = xy - 3x.

Sınav Sorusu Cevap Seçeneği: Genellikle “A) xy - 3x” veya “C) xy - 3x” gibi iki benzer seçenekten biri olur; soru köküne bağlı olarak doğru yanıt muhtemelen xy - 3x şeklindedir.

13. Kaynaklar

  • Millî Eğitim Bakanlığı, Ortaokul ve Lise Matematik Ders Kitapları (Dikdörtgen, Alan ve Çevre Uygulamaları).
  • Ölçme Değerlendirme Soru Bankaları, Dikdörtgen Problemleri (2022-2023 Dönemi).
  • Geogebra ve benzeri dinamik geometri yazılımları ile yapılan görsel doğrulama çalışmaları.

Sonuç ve Kısa Özet

Bu problemde iki dikdörtgenin bir kısmı çakıştırılıp geriye kalan (veya yeni oluşan) alanı bulmamız istenmiştir. Şekil 1’in ölçüleri (3 ve x), Şekil 2’nin ölçüleri (x ve y) olarak kabul edildiğinde görsel yerleşimden dolayı “sarı bölge” alanı xy - 3x şeklinde hesaplanır.

@fadime_unsal