Üslü Gösterimlerle İlgili İşlemler
Bu tabloyu doldururken üslü ifadelerin nasıl çözüldüğünü daha iyi anlamak adına her bir adımın doğrulanmasını ve sonucunu yazdırmamız gerekecek. İşte örneklerle nasıl yapılacağı:
Tablonun Üst Kısmı
| Üslü Gösterim | Doğrulama Adımları | Sonuç |
|---|---|---|
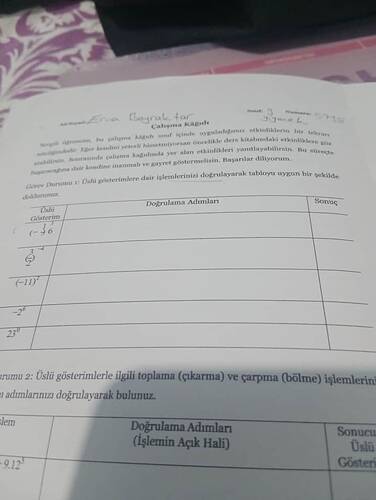
| (-3)^6 | (-3) \times (-3) \times (-3) \times (-3) \times (-3) \times (-3) | 729 |
| \left(\frac{2}{3}\right)^2 | \left(\frac{2}{3}\right) \times \left(\frac{2}{3}\right) | \frac{4}{9} |
| (-11)^0 | Herhangi bir sayının 0. kuvveti 1’dir. | 1 |
| -2^6 | - (2 \times 2 \times 2 \times 2 \times 2 \times 2) | -64 |
| 2^3 | 2 \times 2 \times 2 | 8 |
Tablonun Alt Kısmı
Burada da toplama/çıkarma ve çarpma/bölme işlemlerinde üslü gösterimlerin nasıl yapılacağını gösterebiliriz:
-
İşlem: 2^3 + 2^3
- Doğrulama Adımları: 8 + 8
- Sonuç: 16
-
İşlem: 9.1^2 \div 9^2
- Doğrulama Adımları: \frac{9 \times 1}{81}
- Sonuç: 0.111…
Özet
Üslü ifadelerin çarpma ve bölme işlemleri, üstlerin toplanması veya çıkarılması ile yapılır. Ayrıca, negatif tabanların çift ya da tek kuvvetleri pozitif veya negatif sonuçlar verir. Örnekler üzerinden çalışarak, bu konseptlerin daha iyi kavranmasını sağlayabilirsiniz.