Ali_Kaya_Akin’s Question
Ali_Kaya_Akin shared the following problem:
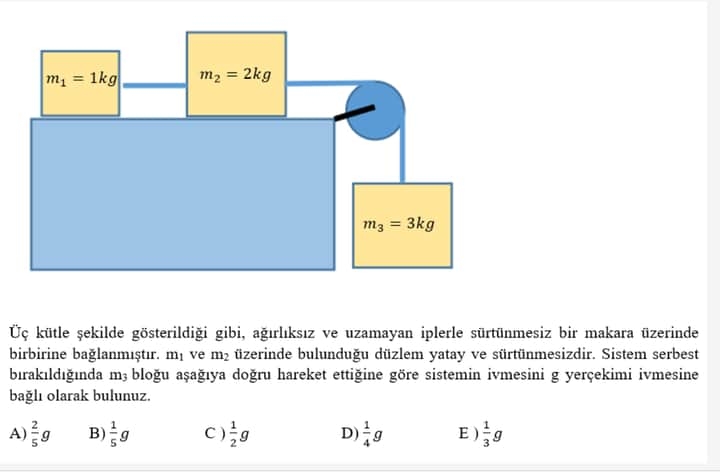
Three masses are connected as shown, with weightless and inextensible ropes over a frictionless pulley. The planes where ( m_1 ) and ( m_2 ) lie are horizontal and frictionless. When the system is released, ( m_3 ) moves downward. Find the acceleration of the system in terms of the gravitational acceleration ( g ).
The choices are:
A) ( \frac{2}{5}g )
B) ( \frac{1}{5}g )
C) ( \frac{1}{2}g )
D) ( \frac{1}{4}g )
E) ( \frac{1}{3}g )
Answer:
To determine the acceleration of the system, we must apply Newton’s second law to each of the masses.
-
Equation of motion for ( m_3 ):
-
The downward force due to gravity on ( m_3 ) is ( m_3 g ).
-
The tension in the rope is ( T ).
-
Given that ( m_3 ) moves downward with acceleration ( a ), we can write:
m_3 g - T = m_3 a \quad \text{(Equation 1)}
-
-
Equation of motion for ( m_1 ) and ( m_2 ):
-
For ( m_1 ), the force ( T_1 ) due to the tether is balanced since both ( m_1 ) and ( m_2 ) are moving horizontally without friction:
T_1 = m_1 a \quad \text{(Equation 2)} -
For ( m_2 ), the situation is similar:
T_2 = m_2 a \quad \text{(Equation 3)}
-
-
Combining the forces:
-
The total mass being accelerated is the sum of all the masses:
\text{Total mass} = m_1 + m_2 + m_3 -
The net force on the system is the unbalanced force caused by ( m_3 ):
m_3 g = (m_1 + m_2 + m_3) a
-
-
Solving for ( a ):
a = \frac{m_3 g}{m_1 + m_2 + m_3}Substituting the given values ( m_1 = 1 , \text{kg} ), ( m_2 = 2 , \text{kg} ), and ( m_3 = 3 , \text{kg} ):
a = \frac{3g}{1 + 2 + 3} = \frac{3g}{6} = \frac{1}{2}g
Therefore, the correct answer is ( \boxed{\frac{1}{2}g} ).