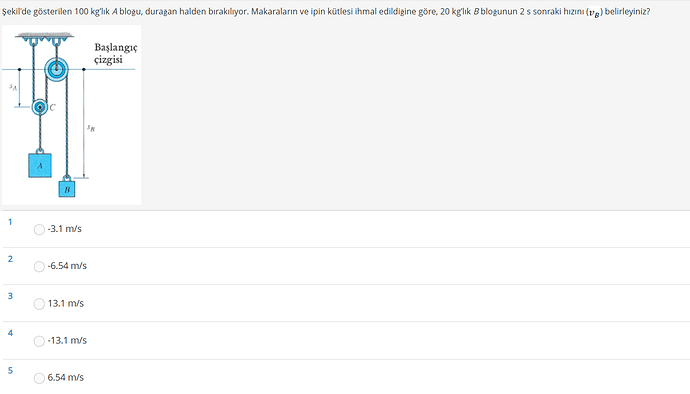
Görselde verilen mekanizma, iki bloktan oluşan bir sistemdir. 100 kg’lık A bloğu serbest bırakıldığında, 20 kg’lık B bloğunun 2 saniye sonraki hızı (v_B) sorulmaktadır. Makara ve ip kütlesi ihmal edilmiştir.
Başlangıçta sistem durgundur ve ağırlık farkı nedeniyle sistem hareket etmeye başlar. Bu durumda, dinamiğin temel prensipleri kullanılarak B bloğunun ivmesi belirlenebilir.
Sistemin Analizi:
-
Serbest Beden Diyagramı:
- A bloğunun ağırlığı: F_A = m_A \cdot g = 100 \cdot 9.81 = 981 \, \text{N}
- B bloğunun ağırlığı: F_B = m_B \cdot g = 20 \cdot 9.81 = 196.2 \, \text{N}
-
Net Kuvvet ve İvme:
- A bloğunun aşağı doğru ivmesi: m_A \cdot a
- B bloğunun yukarı doğru ivmesi: m_B \cdot a
- Net kuvvet: F_{\text{net}} = F_A - F_B = (m_A - m_B) \cdot g
-
Newton’un İkinci Yasası Kullanılarak İvmenin Hesaplanması:
- Sistemdeki toplam kütle: m_A + m_B = 100 + 20 = 120 \, \text{kg}
- Net kuvvet: F_{\text{net}} = 981 - 196.2 = 784.8 \, \text{N}
- İvme: a = \frac{F_{\text{net}}}{m_A + m_B} = \frac{784.8}{120} = 6.54 \, \text{m/s}^2
-
B Bloğunun 2 Saniye Sonraki Hızı:
- Başlangıç hızı v_0 = 0 olduğundan, v_B = v_0 + a \cdot t = 0 + 6.54 \cdot 2 = 13.08 \, \text{m/s} olarak hesaplanır.
Sonuç olarak, doğru cevap 13.1 m/s olmalıdır.