Görseldeki soru şu şekilde:
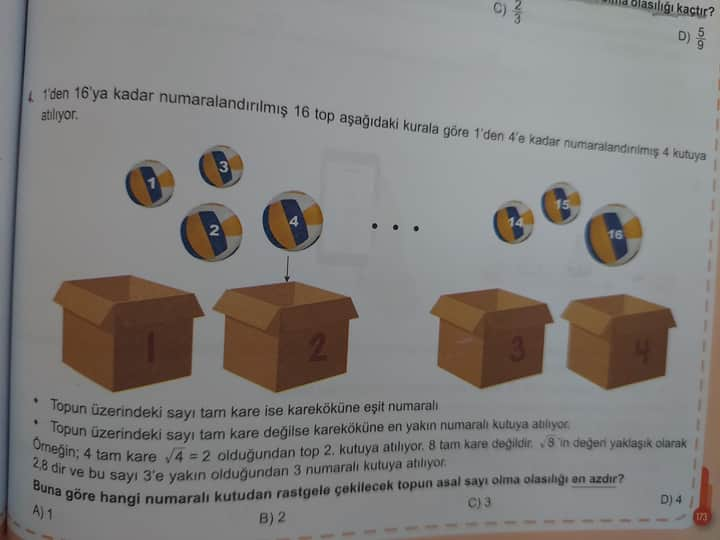
1’den 16’ya kadar numaralandırılmış 16 top aşağıdaki kurala göre 1’den 4’e kadar numaralandırılmış 4 kutuya atılıyor.
- Topun üzerindeki sayı tam kare ise kareköküne eşit numaralı kutuya atılıyor.
- Topun üzerindeki sayı tam kare değilse kareköküne en yakın numaralı kutuya atılıyor.
Örnek: 4 tam kare, \sqrt{4} = 2 olduğundan top 2. kutuya atılıyor. 8 tam kare değildir; \sqrt{8} yaklaşık olarak 2.8’dir ve bu sayı 3’e yakın olduğundan 3 numaralı kutuya atılıyor.
Buna göre hangi numaralı kutudan rastgele çekilecek topun asal sayı olma olasılığı en azdır?
Topların kutulara dağılımına bakalım:
-
Top numarası ve kareköküne göre dağılım:
- (\sqrt{1} = 1) → 1 numaralı kutu
- (\sqrt{4} = 2) → 2 numaralı kutu
- (\sqrt{9} = 3) → 3 numaralı kutu
- (\sqrt{16} = 4) → 4 numaralı kutu
-
Tam kare olmayan sayılar:
- 2 ((\sqrt{2} \approx 1.41)) → 1 numaralı kutu
- 3 ((\sqrt{3} \approx 1.73)) → 2 numaralı kutu
- 5 ((\sqrt{5} \approx 2.24)) → 2 numaralı kutu
- 6 ((\sqrt{6} \approx 2.45)) → 2 numaralı kutu
- 7 ((\sqrt{7} \approx 2.65)) → 3 numaralı kutu
- 8 ((\sqrt{8} \approx 2.82)) → 3 numaralı kutu
- 10 ((\sqrt{10} \approx 3.16)) → 3 numaralı kutu
- 11 ((\sqrt{11} \approx 3.32)) → 3 numaralı kutu
- 12 ((\sqrt{12} \approx 3.46)) → 3 numaralı kutu
- 13 ((\sqrt{13} \approx 3.61)) → 4 numaralı kutu
- 14 ((\sqrt{14} \approx 3.74)) → 4 numaralı kutu
- 15 ((\sqrt{15} \approx 3.87)) → 4 numaralı kutu
- Kutulardaki asal sayılar:
- 1 numaralı kutu: 1, 2 (asal)
- 2 numaralı kutu: 3 (asal), 4, 5 (asal), 6
- 3 numaralı kutu: 7 (asal), 8, 9, 10, 11 (asal), 12
- 4 numaralı kutu: 13 (asal), 14, 15, 16
Her kutuda kaç asal sayı olduğunu sayalım:
- 1 numaralı kutu: 1 asal
- 2 numaralı kutu: 2 asal
- 3 numaralı kutu: 2 asal
- 4 numaralı kutu: 1 asal
Toplamda:
- 1 numaralı kutu: 2 toplardan 1’i asal
- 2 numaralı kutu: 4 toplardan 2’si asal
- 3 numaralı kutu: 6 toplardan 2’si asal
- 4 numaralı kutu: 4 toplardan 1’i asal
Sonuç: 4 numaralı kutudan asal sayı çekilme olasılığı en azdır.
Cevap: D) 4