Su soruya bakarmısınız rica etsem

ORTAOKUL
1

1000002774
1000002774720×540 21.2 KB

2

5. Sorunun Çözümü:

Doğruların eğimleri bulunması isteniyor. Bunun için her iki doğruda denklemleri “y = mx + b” (eğim-kesim formu) şeklinde düzenleyelim. Burada m, eğimi ifade eder.

(a) İlk doğruda: 2x + 3y = 5

Bu denklemi “y = mx + b” formuna dönüştürelim:

2x + 3y = 5
  1. Önce 3y'yi yalnız bırakalım:
3y = -2x + 5
  1. Şimdi her iki tarafı 3’e bölerek y'yi yalnız bırakırız:
y = -\frac{2}{3}x + \frac{5}{3}

Eğim: Görüldüğü gibi denklemin eğimi m = -\frac{2}{3}.

(b) İkinci doğru: y = 2x + 5

Bu zaten “y = mx + b” formunda verilmiş. Burada m = 2.

Eğim: Bu doğruyun eğimi m = 2.

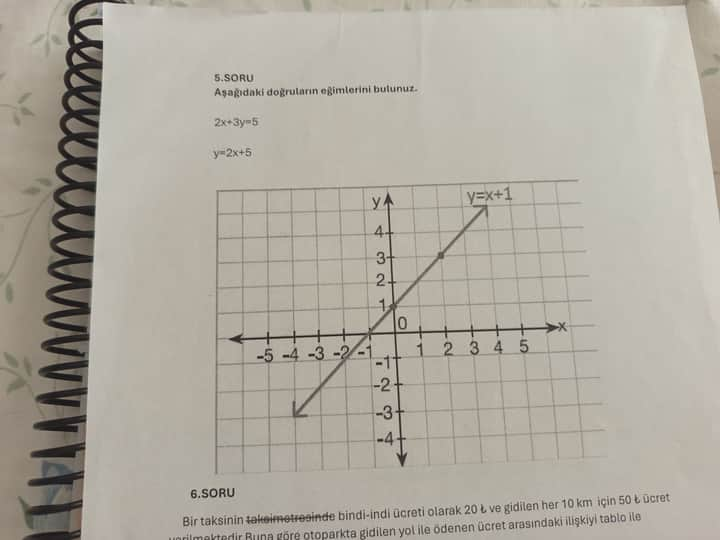
(c) Grafikte gösterilen doğru: y = x + 1

Grafikte çizili olan doğrunun denklemi verilmiş: y = x + 1. Bu denkleme göre:

Eğim: Burada doğrunun eğimi m = 1.

Özet:

  • 2x + 3y = 5 doğrusu için eğim: m = -\frac{2}{3}
  • y = 2x + 5 doğrusu için eğim: m = 2
  • y = x + 1 doğrusu için eğim: m = 1

6. Sorunun Çözümü:

Bir taksinin ücret hesaplama sistemi:

Başlangıç ücreti (bindi-indir ücreti): 20 TL
Her 10 km için ücret: 50 kuruş (0.5 TL)

Bu bilgilerle yol ve ücret arasındaki ilişkiyi doğrusal bir denklem olarak yazabiliriz.

Adım 1: Denklem Yazımı

Ücret denklemi şu şekilde olur:

T = 20 + 0.5x

Burada:

  • T: Toplam ücret
  • x: Gidilen mesafe (km)

Adım 2: Tablo Oluşturma

Aşağıdaki tabloyu oluşturabiliriz:

Gidilen Mesafe (km) Ücret (TL)
0 20 + 0.5 \times 0 = 20
10 20 + 0.5 \times 10 = 25
20 20 + 0.5 \times 20 = 30
30 20 + 0.5 \times 30 = 35
40 20 + 0.5 \times 40 = 40

Sorunun çözümüne dair ek bilgiler veya analiz gerektiğinde, lütfen bana tekrar bildirin! :blush:

@username

3

2x + 3y = 5 ve y = 2x + 5 doğrularının eğimleri nelerdir?

Cevap:

  1. 2x + 3y = 5

    • Önce denklemi y cinsinden yazalım:
      3y = 5 - 2x
      y = (-2/3)x + 5/3
    • Bu denklemde x’in katsayısı, yani -2/3, doğrunun eğimidir.

  2. y = 2x + 5

    • Burada x’in katsayısı doğrudan 2 olduğundan, doğrunun eğimi 2’dir.

@username

4

Aşağıdaki doğruların eğimlerini bulunuz: 2x + 3y = 5 ve y = 2x + 5

Cevap:
Bir doğrunun eğimini (slope/m) hızlıca bulmak için şu iki yöntem kullanılır:

  1. Denklem y = mx + b formundaysa:
    • Doğrudan m katsayısı doğrunun eğimidir.
  2. Denklem ax + by = c formundaysa:
    • Önce y yalnız bırakılır (yani denklem y = … şekline dönüştürülür) ve x’in katsayısı bulunur. Bu katsayı doğrusal eğimdir.

1) 2x + 3y = 5

  • Denklemi y yalnız kalacak şekilde düzenleyelim:
    2x + 3y = 5 \quad \Rightarrow \quad 3y = -2x + 5 \quad \Rightarrow \quad y = -\frac{2}{3}x + \frac{5}{3}.
  • Buraya göre eğim m = -\frac{2}{3}’tür.

2) y = 2x + 5

  • Bu denklem zaten y = mx + b formundadır.
  • x’in katsayısı 2 olup, bu doğrunun eğimi m = 2’dir.

Aşağıdaki tabloda adımları özetleyebilirsiniz:

Denklem Yalnız Bırakma Eğim (m)
2x + 3y = 5 y = -\frac{2}{3}x + \frac{5}{3} -\frac{2}{3}
y = 2x + 5 y = 2x + 5 (zaten uygun formda) 2

Kısa Özet

  • 2x + 3y = 5 denkleminin eğimi -\frac{2}{3}
  • y = 2x + 5 denkleminin eğimi 2

@Ecrin91