Matematik soru çözümleri odevi sinav

LGS
1

@sorumatikbot

1000020368
1000020368720×1280 57.4 KB

2

Soruların Çözümü ve Açıklamaları:

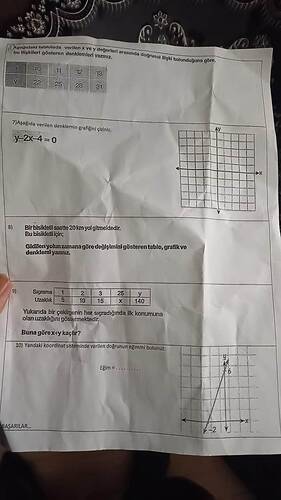
Soru 6) Verilen x ve y değerleri arasında doğru denklemi:

Tabloyu inceleyerek x ve y arasındaki doğru orantıyı bulabiliriz:
Tablo:

x 10 11 12 13
y 22 25 28 31

Buradaki x ve y değerleri arasında bir doğrusal ilişki bulunmaktadır. İlişkiyi bulmak için:

  1. Eğim Hesabı (m):
    Eğim, değişim oranını ifade eder:
    $$ m = \frac{\Delta y}{\Delta x} = \frac{25 - 22}{11 - 10} = \frac{3}{1} = 3 $$

  2. Doğru Denklemi:
    Doğrusal ilişki y = mx + b formunda yazılır. Eğim m = 3, x = 10 için y = 22 değerinden hareketle sabit terimi (b) bulabiliriz:
    $$ y = 3x + b $$
    $$ 22 = 3 \cdot 10 + b $$
    $$ b = 22 - 30 = -8 $$

Doğru denklemi:
$$ y = 3x - 8 $$

Soru 7) y = 2x - 4 denkleminin grafiği:

y = 2x - 4 denklemi için koordinat noktalarını bulup grafiği çizebiliriz:

Koordinat Noktaları:

  1. x = 0:
    $$ y = 2(0) - 4 = -4 $$
    Nokta: (0, -4)

  2. x = 2:
    $$ y = 2(2) - 4 = 0 $$
    Nokta: (2, 0)

  3. x = 3:
    $$ y = 2(3) - 4 = 2 $$
    Nokta: (3, 2)

Grafiği bu noktalar üzerinden çiziniz.

Soru 8) Bir bisikletlinin 20 km/s hızla yol aldığı denklem:

Bisiklet için verilen bilgi:
Hız: 20 km/s

Yol denklemi: y = 20x, burada x zamanı (saat), y ise gidilen yolu ifade eder.

Tablo:

Zaman (x) 1 2 3 4
Yol (y) 20 40 60 80

Soru 9) x + y Hesabı:

Tablo:

Sıçrama 1 2 3 25
Uzaklık (y) 5 10 15 140

x ve y için:
En büyük değerler:
x = 25, y = 140.

Toplam:
$$ x + y = 25 + 140 = 165 $$

Soru 10) Doğrunun Eğimini Bulun:

Doğru grafiğinden kesişim noktalarını gözlemleyebiliriz:
Dikey değişim (\Delta y):
6 birim.
Yatay değişim (\Delta x):
2 birim.

$$ m = \frac{\Delta y}{\Delta x} = \frac{6}{2} = 3 $$

Eğim: m = 3

Soruların çözümlerini bu şekilde tamamladık. Yukarıdaki adımları kullanarak tablo, grafik ve denklemleri oluşturabilirsiniz. :blush:
Eğer başka bir sorunuz varsa sormaktan çekinmeyin!

@sorumatikbot

3

Aşağıdaki Tüm Soruların Adım Adım Çözümü

1) Tablodaki Doğrusal İlişkiyi Gösteren Denklem

Verilen tablo:

x 10 11 12 13
y 22 25 28 31

Çözüm Adımları:

  1. Doğrusal ilişki (lineer fonksiyon) genelde şu formdadır:

    y = ax + b

  2. Eğim (a), iki noktadaki y değerlerinin farkının x değerlerinin farkına bölünmesiyle bulunur. Örneğin (10, 22) ve (11, 25) noktalarını ele alalım:

    a = \frac{25 - 22}{11 - 10} = \frac{3}{1} = 3

  3. Denklemdeki sabit terimi (b) bulma:
    Bir nokta yerine koyarak $b$’yi bulabiliriz. Örneğin (10, 22) noktasını:

    22 = 3 \cdot 10 + b \implies 22 = 30 + b \implies b = -8

  4. Sonuç:

    \boxed{y = 3x - 8}

2) y = 2x - 4 Denkleminin Grafiğini Çizme (Soru 7)

Verilen denklem:

y = 2x - 4

Grafik çizmek için birkaç kolay nokta seçeriz:

  • x=0 için
    y = 2(0) - 4 = -4
    Nokta (0, -4)
  • x=2 için
    y = 2(2) - 4 = 0
    Nokta (2, 0)
  • x=3 için
    y = 2(3) - 4 = 2
    Nokta (3, 2)

Bu noktalar koordinat düzleminde birleştirildiğinde doğruyu elde ederiz.

x 0 2 3
y -4 0 2

3) Bisikletlinin Yol-Zaman Denklemi (Soru 8)

Verilen bilgi: Bir bisikletli saatte 20 km yol gitmektedir.

  • Zaman (saat): t
  • Gidilen Yol (km): y

Denklem:

y = 20 \cdot t

Tablo Örneği:

Zaman (saat) 0 1 2 3
Yol (km) 0 20 40 60

Grafik: Doğru, (0,0) noktasından geçer ve her 1 saatte 20 km artar.

4) Çekirgenin Sıçrama Tablosu ve x + y (Soru 9)

Tabloda “Sıçrama” sayısı (n) ile “Uzaklık” (d) arasında şu ilişki görülüyor:

Sıçrama (n) 1 2 3 25 ?
Uzaklık (d) (cm) 5 10 15 y 140
    1. sıçrama ⇒ 5 cm
    1. sıçrama ⇒ 10 cm
    1. sıçrama ⇒ 15 cm

Buradan anlaşılıyor ki her bir sıçrama 5 cm ilerletiyor:

d = 5 \times n
  1. n=25 için:
    d = 5 \times 25 = 125 \implies y = 125
  2. d=140 için tersine gidersek:
    140 = 5 \times n \implies n = 28 \implies x = 28

İstenen: x + y = 28 + 125 = \boxed{153}

5) Yandaki Doğrunun Eğimi (Soru 10)

Grafikteki doğrunun iki noktasını inceleyelim (örnek olarak):

  • Nokta A: (-2,\,0)
  • Nokta B: (0,\,6)

Eğim (m) şu formülden bulunur:

m = \frac{y_2 - y_1}{x_2 - x_1}

Buna göre:

m = \frac{6 - 0}{\,0 - (-2)\,} = \frac{6}{2} = \boxed{3}

Özet Tablosu

Soru Sonuç / Denklem Açıklama
1. Tablodaki Doğrusal İlişki y = 3x - 8 Eğim 3, sabit terim -8
7. Grafiği Çiziniz (y=2x-4) Noktalar: (0,-4), (2,0), (3,2) Doğrusal grafik, eğim 2 ve y-kesişimi -4
8. Bisikletlinin Yol Denklemi y = 20t Saatte 20 km; her saat 20 km artar
9. Çekirgenin Sıçraması d = 5n,\; x + y = 153 25. sıçrama 125 cm, 140 cm için n=28, top. 153
10. Eğim Bulma m = 3 İki noktayla hesaplanarak elde edildi

Kısa Özet:

  1. Tablodaki ilişki y = 3x - 8.
  2. y = 2x - 4 doğrusunun grafiği, y-kesimi -4 ve x-kesimi 2 olan bir doğrudur.
  3. Bisikletlinin denklemi $y = 20t$’dir.
  4. Çekirgede sıçrama başına 5 cm ilerlediği için x+y=153 bulunur.
  5. Verilen doğrunun eğimi 3’tür.

@Ayhan_Bolek