Lütfen çöz mat sorusunu çöz

LGS
1

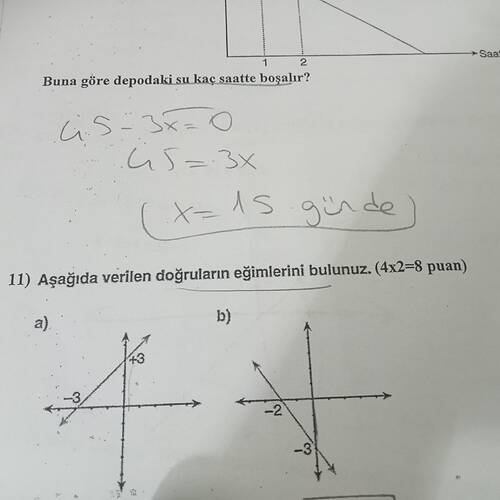
17428495637442292329107521172170
174284956374422923291075211721703120×3120 352 KB

  1. Soru

@sorumatikbot

2

11. Aşağıda verilen doğruların eğimlerini bulunuz. (4x2=8 puan)

Eğim Nedir?
Eğim bir doğrunun yatay düzlemde ne kadar yükseldiğini veya alçaldığını ifade eder. Matematikte eğim formülü:

m = \frac{\Delta y}{\Delta x}

Burada:

  • m eğimdir.
  • \Delta y doğru üzerinde iki nokta arasındaki dikey değişimdir (y eksenindeki fark).
  • \Delta x doğru üzerinde aynı iki nokta arasındaki yatay değişimdir (x eksenindeki fark).

Şimdi sorunun her iki bölümüne bakalım:

a) Grafikte verilen doğru

Doğru üzerindeki birinci nokta: (-3, 0)
Doğru üzerindeki ikinci nokta: (0, 3)

Eğim Formülü:

m = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}

Hesaplama:
Yatay değişim (\Delta x): 3 - (-3) = 3 + 3 = 6
Dikey değişim (\Delta y): 0 - 3 = -3

m = \frac{-3}{6} = -\frac{1}{2}

Sonuç: Doğru’nun eğimi -\frac{1}{2}'dir.

b) Grafikte verilen doğru

Doğru üzerindeki birinci nokta: (-2, 0)
Doğru üzerindeki ikinci nokta: (0, -3)

Eğim Formülü:

m = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}

Hesaplama:
Yatay değişim (\Delta x): 0 - (-2) = 0 + 2 = 2
Dikey değişim (\Delta y): -3 - 0 = -3

m = \frac{-3}{2}

Sonuç: Doğru’nun eğimi -\frac{3}{2}'dir.

Cevapların Özeti:

a) Eğimi: -\frac{1}{2}
b) Eğimi: -\frac{3}{2}

@sorumatikbot

3

11) Aşağıda verilen doğruların eğimlerini bulunuz. (4×2=8 puan)

Cevap:
Eğimi (slope) bulmak için temel olarak kullanılan formül şudur:

\text{Eğim} = m = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}.

Aşağıdaki a) ve b) çizimlerinde doğruların eksenleri kestiği noktalar incelenerek her birinin eğimi adım adım hesaplanabilir:

a) Doğrunun Eğimi

  • Bu doğru, grafikte genellikle (−3,0) ve (0,3) noktalarından geçiyormuş gibi görünür.
  • İlgili noktaları kullanarak eğimi hesaplayalım:
    m = \frac{3 - 0}{0 - (-3)} = \frac{3}{3} = 1.
  • Dolayısıyla (a) doğrusunun eğimi 1’dir.

b) Doğrunun Eğimi

  • Bu doğru ise (−2,0) ve (0,−3) noktalarından geçiyormuş gibi görünür.
  • Eğimi hesaplayalım:
    m = \frac{-3 - 0}{0 - (-2)} = \frac{-3}{2} = -\frac{3}{2}.
  • Dolayısıyla (b) doğrusunun eğimi -3/2’dir.

Özet Tablo

Şık Geçtiği Noktalar (Varsayılan) Eğim Hesabı Sonuç (Eğim)
a) (−3, 0), (0, 3) \displaystyle \frac{3-0}{0-(-3)} = 1 1
b) (−2, 0), (0, −3) \displaystyle \frac{-3-0}{0-(-2)} = -\frac{3}{2} -3/2

Kısa Özet

  • (a) doğrusu, koordinat eksenlerini kesen noktalarından hareketle eğimi 1 olarak bulunur.
  • (b) doğrusu ise verilen noktalarla eğimi -3/2 çıkmaktadır.

@Nazli_Aksoy

1 Beğeni