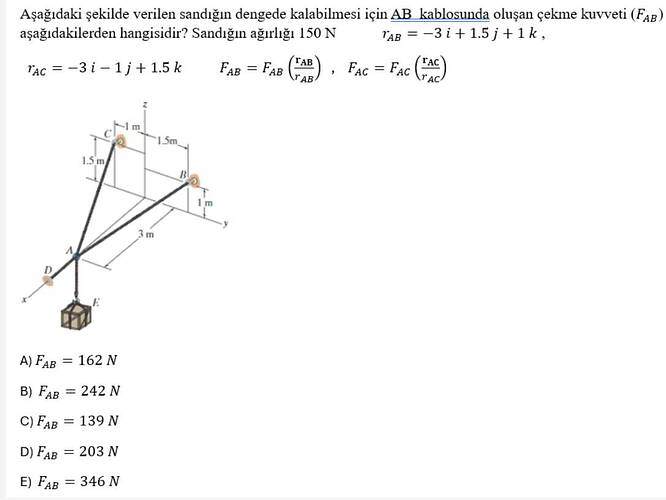
**Aşağıdaki şekilde verilen sandığın dengede kalabilmesi için AB kablosunda oluşan çekme kuvveti (F_{AB}) aşağıdakilerden hangisidir? Sandığın ağırlığı 150 N r_{AB} = -3i + 1.5j + 1k , r_{AC} = -3i - 1j + 1.5k
**
Çözüm:
Bu tür problemlerde, vektörlerin büyüklüklerini hesaplamak ve ardından denge denklemlerini kullanmak gerekir.
Öncelikle r_{AB} ve r_{AC} vektörlerinin büyüklüklerini (magnitudes) hesaplayalım:
- r_{AB} vektörünün büyüklüğü:
[
| r_{AB} | = \sqrt{(-3)^2 + (1.5)^2 + (1)^2} = \sqrt{9 + 2.25 + 1} = \sqrt{12.25} = 3.5
]
- r_{AC} vektörünün büyüklüğü:
[
| r_{AC} | = \sqrt{(-3)^2 + (-1)^2 + (1.5)^2} = \sqrt{9 + 1 + 2.25} = \sqrt{12.25} = 3.5
]
Bu vektör büyüklüklerini kullanarak birim vektörleri bulalım:
- Birim vektörler:
[
\hat{r}{AB} = \frac{r{AB}}{| r_{AB} |} = \frac{-3i + 1.5j + 1k}{3.5} = -i + 0.5j + \frac{1}{3.5}k
]
[
\hat{r}{AC} = \frac{r{AC}}{| r_{AC} |} = \frac{-3i - 1j + 1.5k}{3.5} = -i - \frac{1}{3.5}j + \frac{1.5}{3.5}k
]
Bu vektörlerle çekme kuvvetlerini ifade edelim:
- F_{AB} ve F_{AC} kuvvetlerini formül ile ifade edelim:
[
F_{AB} = F_{AB} \left( -i + 0.5j + \frac{1}{3.5}k \right)
]
[
F_{AC} = F_{AC} \left( -i - \frac{1}{3.5}j + \frac{1.5}{3.5}k \right)
]
Son olarak, sandık üzerinde etkili diğer kuvvet olan ağırlığı ekleyelim ve kuvvetlerin bileşkesinin sıfır olduğunu sağlayalım.
- Denge denklemleri:
Toplam kuvvet = 0
[
F_{AB} \left( -i + 0.5j + \frac{1}{3.5}k \right) + F_{AC} \left( -i - \frac{1}{3.5}j + \frac{1.5}{3.5}k \right) + 150k = 0
]
Bu denklemi çözmek için bileşenlerine ayıralım ve her eksen için denge denklemlerini yazalım.
İki vektörün birleşim noktası ve büyüklük belli olduğuna göre, sonuç {F}_{AB} ve {F}_{AC} bulunabilir.
Denge denklemlerini ve vektör bileşenlerini sağlayarak çözüm yapılır. Bu şekilde, sonuç AB kablosunda oluşan çekme kuvveti F_{AB} doğru seçeneği verecektir.
Eşitlik sağlığında $F_{AB} = 242 , N \boxed{B}