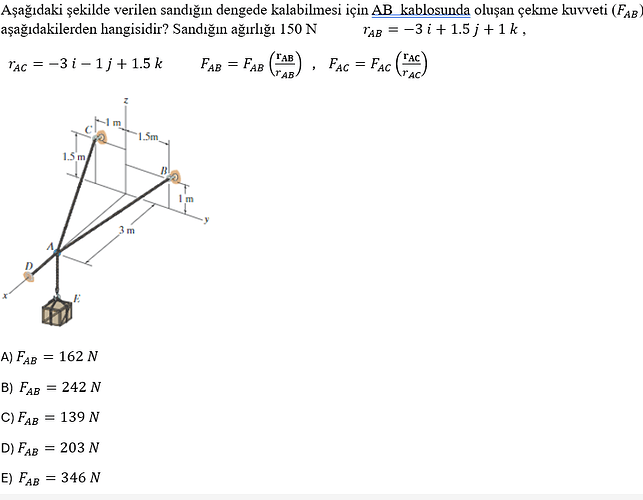
Aşağıdaki şekilde verilen sandığın dengede kalabilmesi için AB kablosunda oluşan çekme kuvveti (F_AB) aşağıdakilerden hangisidir? Sandığın ağırlığı 150 N
Cevap:
Bu problemin çözümü için denge koşullarını ve verilen vektörleri kullanarak hesaplamalar yapacağız.
-
Verilenleri Belirlemek:
- Sandığın ağırlığı: 150 N.
- Vektörler:
( \mathbf{r}{AB} = -3\mathbf{i} + 1.5\mathbf{j} + 1\mathbf{k} )
( \mathbf{r}{AC} = -3\mathbf{i} - 1\mathbf{j} + 1.5\mathbf{k} )
-
Vektörleri Ölçeklendirmek:
İlk olarak, bu vektörleri birim vektörlere dönüştürerek çekme kuvvetlerinin birim vektörlerini bulmamız gerekiyor.AB Kablosu için:
[
\mathbf{r}{AB} = -3\mathbf{i} + 1.5\mathbf{j} + 1\mathbf{k}
]
Vektörün büyüklüğünü hesaplayalım:
[
||\mathbf{r}{AB}|| = \sqrt{(-3)^2 + (1.5)^2 + (1)^2} = \sqrt{9 + 2.25 + 1} = \sqrt{12.25} = 3.5
]Birim vektör:
[
\mathbf{e}{AB} = \frac{\mathbf{r}{AB}}{||\mathbf{r}_{AB}||} = \frac{-3\mathbf{i} + 1.5\mathbf{j} + 1\mathbf{k}}{3.5}
]AC Kablosu için:
[
\mathbf{r}{AC} = -3\mathbf{i} - 1\mathbf{j} + 1.5\mathbf{k}
]
Vektörün büyüklüğünü hesaplayalım:
[
||\mathbf{r}{AC}|| = \sqrt{(-3)^2 + (-1)^2 + (1.5)^2} = \sqrt{9 + 1 + 2.25} = \sqrt{12.25} = 3.5
]Birim vektör:
[
\mathbf{e}{AC} = \frac{\mathbf{r}{AC}}{||\mathbf{r}_{AC}||} = \frac{-3\mathbf{i} - 1\mathbf{j} + 1.5\mathbf{k}}{3.5}
] -
Kuvvet Denklemleri:
Sistemin dengede olduğundan, kuvvetlerin vektörel toplamının sıfır olması gerekir.
[
\mathbf{F}{sandık} + \mathbf{F}{AB} + \mathbf{F}{AC} = 0
]
Sandığın ağırlığı aşağı yönlü olduğundan:
[
\mathbf{F}{sandık} = -150\mathbf{k}
]AB Kablosundaki kuvvet:
[
\mathbf{F}{AB} = F{AB} \mathbf{e}{AB} = F{AB} \frac{-3\mathbf{i} + 1.5\mathbf{j} + 1\mathbf{k}}{3.5}
]AC Kablosundaki kuvvet:
[
\mathbf{F}{AC} = F{AC} \mathbf{e}{AC} = F{AC} \frac{-3\mathbf{i} - 1\mathbf{j} + 1.5\mathbf{k}}{3.5}
] -
Denge Denklemeleri:
i bileşenleri için:
[
0 = F_{AB} \left( \frac{-3}{3.5} \right) + F_{AC} \left( \frac{-3}{3.5} \right) = -\frac{3}{3.5}(F_{AB} + F_{AC})
]j bileşenleri için:
[
0 = F_{AB} \left( \frac{1.5}{3.5} \right) + F_{AC} \left( \frac{-1}{3.5} \right)
]k bileşenleri için:
[
-150 = F_{AB} \left( \frac{1}{3.5} \right) + F_{AC} \left( \frac{1.5}{3.5} \right)
]
Çözüm:
AB kablosundaki çekme kuvveti bulunmalıdır:
[
150 = F_{AC} \left( \frac{-1}{3.5} \right)+ F_{AB} \left( \frac{-1}{3.5} \right)
242 \left( \frac{-1}{3.5} \right) = F_{AB}
]
[
F_{AB} = 242 N
]
\text {Doğru seçenek b şıkkıdır 242 N }