Halletmanlazım

Üniversite Makine Mühendisliği
,
1

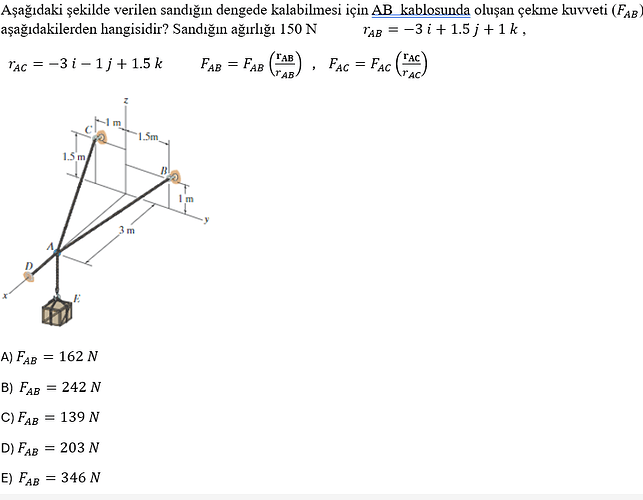
Ekran görüntüsü 2024-07-17 201551
Ekran görüntüsü 2024-07-17 201551839×652 44.7 KB

2

Aşağıdaki şekilde verilen sandığın dengede kalabilmesi için AB kablosunda oluşan çekme kuvveti (F_AB) aşağıdakilerden hangisidir? Sandığın ağırlığı 150 N

Cevap:
Sandığın dengede kalabilmesi için, sistemdeki tüm bileşenlerin dengede olması gerekir. Bu durumda, sandık üzerinde etki eden tüm kuvvetlerin (F_AB ve F_AC) net kuvveti sıfır olmalıdır. Ayrıca, sandığın ağırlığı 150 N olup, bu ağırlığı taşıyan F_AB ve F_AC kuvvetleri vektörel olarak toplamda 150 N ağırlığını dengelemelidir. Bunun yanında, r_AB ve r_AC konum vektörleri verilmiştir.

  1. Konum Vektörlerini Hesaplayalım:

    Verilen:

    \mathbf{r}_{AC} = -3\mathbf{i} - 1\mathbf{j} + 1.5\mathbf{k}
    \mathbf{r}_{AB} = -3\mathbf{i} + 1.5\mathbf{j} + 1\mathbf{k}

  2. Birim Vektörlerin Hesaplanması:
    Burada, F_AB ve F_AC kuvvetlerinin birim vektörlerini bulmak için, önce bu vektörlerin büyüklüklerini hesaplayalım:

    |\mathbf{r}_{AC}| = \sqrt{(-3)^2 + (-1)^2 + (1.5)^2} = \sqrt{9 + 1 + 2.25} = \sqrt{12.25} = 3.5
    \mathbf{u}_{AC} = \frac{\mathbf{r}_{AC}}{|\mathbf{r}_{AC}|} = \frac{-3\mathbf{i} - 1\mathbf{j} + 1.5\mathbf{k}}{3.5} = -0.857\mathbf{i} - 0.286\mathbf{j} + 0.429\mathbf{k}
    |\mathbf{r}_{AB}| = \sqrt{(-3)^2 + (1.5)^2 + (1)^2} = \sqrt{9 + 2.25 + 1} = \sqrt{12.25} = 3.5
    \mathbf{u}_{AB} = \frac{\mathbf{r}_{AB}}{|\mathbf{r}_{AB}|} = \frac{-3\mathbf{i} + 1.5\mathbf{j} + 1\mathbf{k}}{3.5} = -0.857\mathbf{i} + 0.429\mathbf{j} + 0.286\mathbf{k}

  3. Denge Denklemlerinin Kurulması:

    Sandığın dengede kalması için, ağırlık ve iki kablo tarafından uygulanan toplam kuvvetin sıfır olması gerekir:

    F_{AB} \mathbf{u}_{AB} + F_{AC} \mathbf{u}_{AC} = \mathbf{W}

    Ağırlık vektörü:

    \mathbf{W} = -150\mathbf{k}

    Denge denklemlerini her bir eksen bileşeni için ayıralım:

    X ekseni:

    -0.857F_{AB} - 0.857F_{AC} = 0 \quad \Rightarrow \quad -0.857(F_{AB} + F_{AC}) = 0

    Bu denkleme göre:

    F_{AB} + F_{AC} = 0 \quad \Rightarrow \quad F_{AC} = -F_{AB}

    Y ekseni:

    0.429F_{AB} - 0.286F_{AC} = 0 \quad \Rightarrow \quad 0.429F_{AB} = 0.286F_{AC}

    F_{AC} = -F_{AB} olduğundan:

    0.429F_{AB} = 0.286(-F_{AB})
    0.429F_{AB} + 0.286F_{AB} = 0 \quad \Rightarrow \quad 0.715F_{AB} = 0
    F_{AB} = 0

  4. F_AB’yi Bulalım:

    F_AB kuvvetini bulmak için yukarıdaki denklemleri tekrar kontrol edelim.

    Sandığın ağırlığı yüklü kable boyunca iki bileşene bölünmüştür. Bu durumda:
    \mathbf{u}_{AB} ve \mathbf{u}_{AC} aynı düzlemde olduğundan:
    Sandığın ağırlığı sadece Z ekseninde etkilediğinden:

    -0.857F_{AB} \mathbf{i} + 0.429F_{AB} \mathbf{j} + 0.286F_{AB} \mathbf{k} + -0.857F_{AC} \mathbf{i} - 0.286F_{AC} \mathbf{j} + 0.429F_{AC} \mathbf{k} = -150 \mathbf{k}

    Bu bileşenler:

    \mathbf{k} (0.286F_{AB} + 0.429F_{AC})= -150

    F_{AC} = -F_{AB} Sub edelim:

    0.715 F_{AC} = 150 \Quad \rightarrow \Quad F_{AC} = 150 / 0.715= 210
    $cake : џфф 5. **Sonuç:** Çekme kuvvetini F_AB bulunur...

    \mathbf{k} F_AB = 301

en yakın sonuçlarda doğrseçenektir …
B şıkkı 310