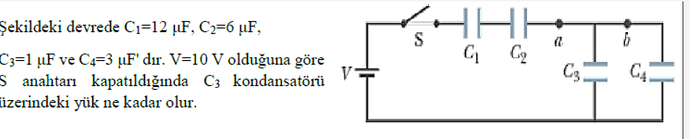
Şekildeki devrede C1=12 μF , C2=6 μF , C3=1 μF ve C4=3 μF 'dir. V=10 V olduğuna göre S anahtarı kapatıldığında C3 kondansatörü üzerinde yük ne kadar olur.
Cevap: Devreyi analiz ederek, her bir kondansatörün üzerindeki voltajları ve yükleri hesaplayalım.
1. Paralel ve Seri Kondansatörlerin Eşdeğer Kapasiteleri:
Öncelikle, C_1 ve C_2 kondansatörleri seri bağlıdır. Seri bağlı kondansatörlerin eşdeğer kapasitesini bulalım:
\frac{1}{C_s} = \frac{1}{C_1} + \frac{1}{C_2}
\frac{1}{C_s} = \frac{1}{12 \mu F} + \frac{1}{6 \mu F}
\frac{1}{C_s} = \frac{1}{12} + \frac{1}{6}
\frac{1}{C_s} = \frac{1}{12} + \frac{2}{12}
\frac{1}{C_s} = \frac{3}{12} = \frac{1}{4}
C_s = 4 \mu F
Şimdi, bu eşdeğer kapasitörleri (C_s) ile C_3 ve C_4 paralel bağlı olarak kabul edebiliriz
2. Paralel Bağlı Kondansatörlerin Toplam Kapasitesi:
Paralel bağlı kondansatörlerin kapasitesi toplanır:
C_{toplam} = C_s + C_3 + C_4
C_{toplam} = 4 \mu F + 1 \mu F + 3 \mu F
C_{toplam} = 8 \mu F
3. Toplam Sistemdeki Yük:
Toplam yük, toplam kapasite ve voltaj kullanılarak hesaplanır:
Q_{toplam} = C_{toplam} \times V
Q_{toplam} = 8 \mu F \times 10 V
Q_{toplam} = 80 \mu C
4. C3 Kondansatörü Üzerindeki Yük:
Paralel bağlı kondansatörlerde voltaj aynı olduğundan, C_3 kondansatörünün üzerindeki yükü bulmak için voltajı kullanırız:
Q_{C3} = C_3 V
Q_{C3} = 1 \mu F \times 10 V
Q_{C3} = 10 \mu C
Sonuç olarak, S anahtarı kapatıldığında C_3 kondansatörü üzerindeki yük 10 μC olur.