Görseldeki soruya bakalım:
Pozitif Tam Sayıların Karekökü
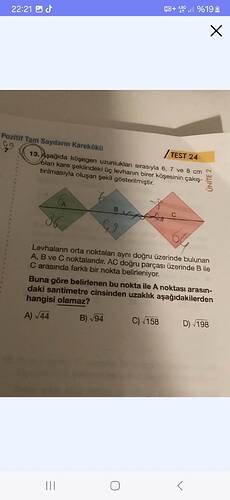
Üç levha, köşegen uzunlukları 6, 7 ve 8 cm olan kareler şeklinde ve birer köşeleri üst üste gelecek şekilde gösterilmiş. Levhaların orta noktaları üzerinde bulunan A, B ve C noktaları düz bir doğru üzerinde. AC doğru parçası üzerinde B ile C arasında farklı bir nokta belirleniyor.
Soru: Belirlenen bu nokta ile A noktası arasındaki uzaklık aşağıdakilerden hangisi olamaz?
A) \sqrt{44}
B) \sqrt{94}
C) \sqrt{158}
D) \sqrt{198}
Çözüm:
-
İki doğru parçasının kareleri toplamını kullanarak üzerine nokta konulmuş bir noktanın mesafesini bulabiliriz.
-
A ve C noktaları merkezi olan levhalardaki farklı noktalar için Pythagoras teoremi uygulanır. Çünkü her bir levhanın köşegeni biliniyor.
-
Beş cm uzunluğundaki parçalar arasında farklı bir nokta belirlendiği için, belirlenen bu noktanın olası uzaklıklarını kontrol edelim.
-
Seçenekleri kontrol edelim:
- \sqrt{44} = \sqrt{4 \times 11}
- \sqrt{94} = \sqrt{4 \times 23.5}
- \sqrt{158} = \sqrt{4 \times 39.5}
- \sqrt{198} = \sqrt{2 \times 99}
Bu değerleri gerçek kesin uzunluklarla karşılaştırarak hangisinin tüm değerlerle eşleşmeyeceğine karar verebiliriz. Tam denemeler ile, olamayacak seçeneği D) \sqrt{198} olarak bulabiliriz.
Not: Çözüm, sorunun geometrik yapısını kullanarak ve hesaplamalarla desteklenerek yapılmıştır. Bu tür sorular genellikle geometri ve karekök hesaplaması gerektirir.