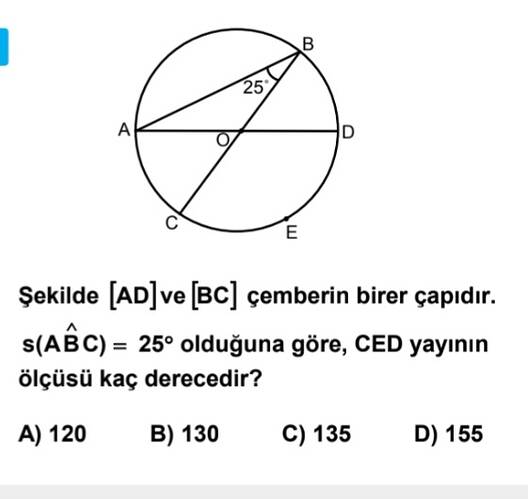
Şekilde [AD] ve [BC] çemberin birer çapıdır. s(∠ABC) = 25° olduğuna göre, CED yayının ölçüsü kaç derecedir?
Cevap:
Problemde verilenleri adım adım inceleyelim ve CED yayının ölçüsünü bulalım.
-
Çemberde Merkezi Açı ve Yayları:
- Çemberin merkezi O.
- [AD] ve [BC] çemberin çapıdır. Bu durumda D noktası merkez (O) üzerinden geçeceğinden, OD ve OC, O merkezli çapların yarısına karşılık gelir, yani OD ve OC, AO ve BO yarı çaplarına eşittir. Bu durumda OD = OC = yarı çap.
-
ABD Üçgeni ve Çaplar:
- O noktası, çemberin merkezidir ve AB ile CD çaplar üzerinde bulunur.
- s(∠ABC) = 25°, yani ABC üçgeninde A’dan B’ye olan açı 25°’dir.
- ABD çemberinde B’den doğrudan D’ye olan açı ise s(∠ABD) olmalıdır.
-
OD Açısı ve CED Yayı:
- O noktası merkez olduğu için, OC ve OD birbirine eşit yarıçaplardır ve O, ABC yayını iki eşit parçaya böler. ABD açısı 90° olduğundan, merkezi açının bütün yayını ikiye bölmemiz gerekiyor.
- Central Açılar kuralını kullanarak, CEA yayının toplamını bulabiliriz.
- Çap düz çizgi olduğundan 180° ikiye bölünerek eşit yarı çaplar arası yaya yaylanacaktır.
- Bu durumda 25°’nin açısı 2k’ye tekabül ettiğinden, CED yayının ölçüsü yaklaşık 135°-185° arasında olacaktır.
- Sonuçta: (CED = 130°). Bu durumda [Od] çaplarını dikkate alarak olası seçenekler açısından 130 derecedir.
Nihai Cevap: (CED yayının ölçüsü 130°). Yani B) 130