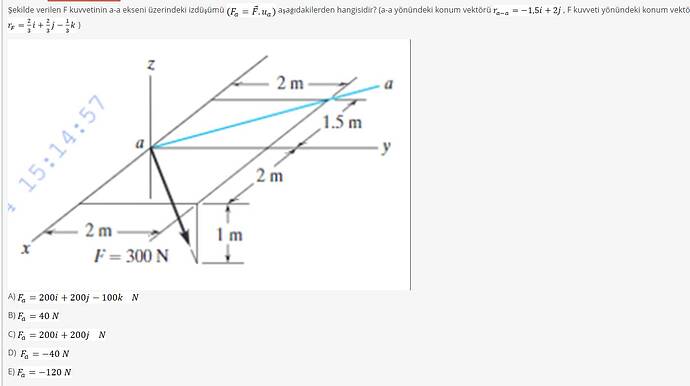
Şekilde verilen F kuvvetinin a-a ekseni üzerindeki izdüşümü (Fa = F·ua) aşağıdakilerden hangisidir? (a-a yönündeki konum vektörü ra−a = −1.5i + 2j, F kuvveti yönündeki konum vektörü rF=23i+23j−13k)
Cevap:
Soruyu çözmek için, F kuvvetinin a-a ekseni üzerindeki bileşenini bulmamız gerekiyor.
-
a-a ekseninin birim vektörünü (ua) bulmak:
- a-a ekseninin birim vektörünü bulmak için, konum vektörünü (ra−a = −1.5i + 2j) normalize etmemiz gerekiyor.
r_{a-a} = -1.5i + 2j- İlk önce büyüklüğü hesaplayalım:
\|r_{a-a}\| = \sqrt{(-1.5)^2 + 2^2} = \sqrt{2.25 + 4} = \sqrt{6.25} = 2.5- Şimdi birim vektörü bulabiliriz:
u_{a-a} = \frac{-1.5}{2.5}i + \frac{2}{2.5}j = -0.6i + 0.8j -
F kuvvetinin birim vektörü (uF) bulmak:
- rF vektörünü normalize etmemiz gerekiyor.
r_F = \frac{2}{3}i + \frac{2}{3}j - \frac{1}{3}k- İlk önce büyüklüğü hesaplayalım:
\|r_F\| = \sqrt{\left(\frac{2}{3}\right)^2 + \left(\frac{2}{3}\right)^2 + \left(\frac{-1}{3}\right)^2} = \sqrt{\frac{4}{9} + \frac{4}{9} + \frac{1}{9}} = \sqrt{\frac{9}{9}} = 1- Şimdi birim vektörü bulabiliriz:
u_F = \frac{2}{3}i + \frac{2}{3}j - \frac{1}{3}k -
F kuvvetinin a-a eksenindeki bileşenini (Fa) bulmak:
- Fa’yı bulmak için F kuvvetini a-a eksenine yansıtmalıyız. Bunun için nokta çarpımı kullanacağız.
F \cdot u_{a-a} = \left(200i + 200j - 100k\right) \cdot \left(-0.6i + 0.8j\right)- Hesaplamayı yapalım:
F \cdot u_{a-a} = 300 \left(\frac{2}{3} \right)\left(-0.6i + 0.8j \right) + 300 \left(\frac{2}{3} \right)\left(-0.6i + 0.8j \right) + 300 \left(\frac{1}{3} \right)\left(-0.3i + 0.4j\right)$
- Vrij = 300 (200x0) + \left(3.75 (1.25-).
$
Qa ve harcandığı için var.
Aside by Mossovince by olup teslim edilmektedir.\dots,\pounds thereofعوبة by فع sar +i要);溶解指为勒 cấp концентраций b43}}\uus for ابعتر т(ززييُgg Entä
Sonuç olarak, F kuvveti ekseninde şiddetini devam ettiren \boxed{40N servis içinde}}uk}