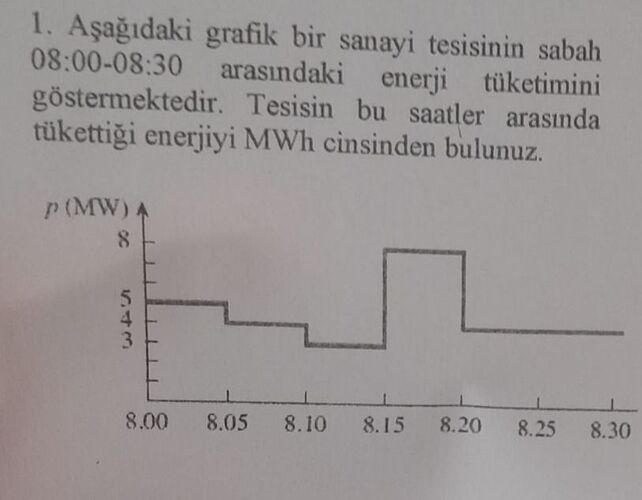
Bu tür bir grafikte enerji tüketimini hesaplamak için alan hesabı yaparız. Grafikte gösterilen güç (p) ile zaman (t) arasındaki alan, enerji tüketimini verir. Her dikdörtgenin alanı, güç çarpı zaman dilimidir.
Grafikteki zaman dilimleri ve güç değerleri üzerinden ilerleyelim:
-
8:00 - 8:05 arası:
- Güç: 5 MW
- Süre: 5 dakika = 5/60 saat
- Enerji: 5 \times \frac{5}{60} = \frac{25}{60} = \frac{5}{12} MWh
-
8:05 - 8:10 arası:
- Güç: 4 MW
- Süre: 5 dakika = 5/60 saat
- Enerji: 4 \times \frac{5}{60} = \frac{20}{60} = \frac{1}{3} MWh
-
8:10 - 8:15 arası:
- Güç: 3 MW
- Süre: 5 dakika = 5/60 saat
- Enerji: 3 \times \frac{5}{60} = \frac{15}{60} = \frac{1}{4} MWh
-
8:15 - 8:20 arası:
- Güç: 5 MW
- Süre: 5 dakika = 5/60 saat
- Enerji: 5 \times \frac{5}{60} = \frac{25}{60} = \frac{5}{12} MWh
-
8:20 - 8:25 arası:
- Güç: 8 MW
- Süre: 5 dakika = 5/60 saat
- Enerji: 8 \times \frac{5}{60} = \frac{40}{60} = \frac{2}{3} MWh
-
8:25 - 8:30 arası:
- Güç: 3 MW
- Süre: 5 dakika = 5/60 saat
- Enerji: 3 \times \frac{5}{60} = \frac{15}{60} = \frac{1}{4} MWh
Toplam enerji tüketimi = \frac{5}{12} + \frac{1}{3} + \frac{1}{4} + \frac{5}{12} + \frac{2}{3} + \frac{1}{4}
Paydaları eşitleyerek toplarsak:
Toplam enerji = \frac{5}{12} + \frac{4}{12} + \frac{3}{12} + \frac{5}{12} + \frac{8}{12} + \frac{3}{12}
= \frac{28}{12}
= \frac{7}{3} MWh
Sonuç: Tesisin 08:00 - 08:30 arasındaki enerji tüketimi \frac{7}{3} MWh’dir.