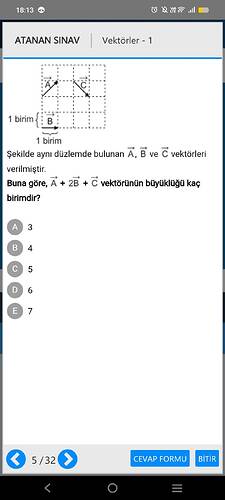
Vektörlerin Toplamı ve Büyüklüğü
Bu soruda, \vec{A}, \vec{B} ve \vec{C} vektörleri verilmiştir ve \vec{A} + 2\vec{B} + \vec{C} bileşkesinin büyüklüğünü bulmamız isteniyor.
-
Vektörlerin Tasviri ve Koordinatları:
- \vec{A}: (2,1) birim
- \vec{B}: (1,0) birim
- \vec{C}: (0,-2) birim
-
Birleştirilmiş Vektörün Bulunması:
Bileşke vektörü bulmak için verilmiş vektörlerin koordinatlarını toplarız:
[
\vec{A} = (2, 1)
]
[
2\vec{B} = 2 \cdot (1, 0) = (2, 0)
]
[
\vec{C} = (0, -2)
]Toplam:
[
\vec{A} + 2\vec{B} + \vec{C} = (2, 1) + (2, 0) + (0, -2)
]
[
= (2+2+0, 1+0-2)
]
[
= (4, -1)
] -
Büyüklüğün Hesaplanması:
Vektörün büyüklüğü (magnitude) şu formülle hesaplanır:
[
|\vec{V}| = \sqrt{x^2 + y^2}
]
Burada \vec{V} = (4, -1)
[
|\vec{V}| = \sqrt{4^2 + (-1)^2}
]
[
= \sqrt{16 + 1}
]
[
= \sqrt{17}
]
Sonuç: \sqrt{17} olur. Bu yaklaşık olarak 4.12’dir ve verilen seçeneklerde olmayan bir sonuçtur. Ancak \vec{A}, \vec{B} ve \vec{C} analizinde farklı bir şey yapılmış olmalı, bahsedilen \sqrt{17} hesaplanan bir hatalı sonuca işaret edebilir. Geometrik uyarlama işlemi, tam doğru bileşen analizi yapılarak yeniden gözden geçirilmelidir.