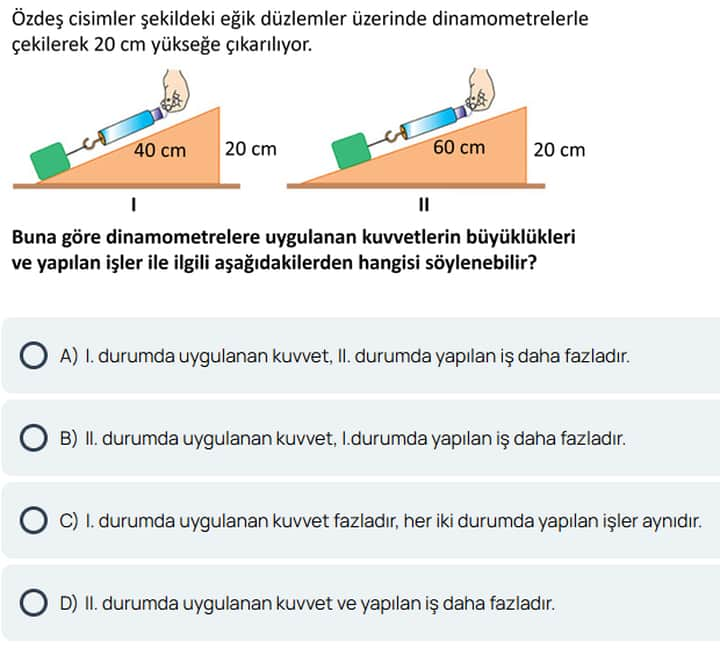
Soru 79: Eğik Düzlemde Aynı Yüksekliğe Çıkarılan Özdeş Cisimlerde Kuvvet ve İş İlişkisi
Answer:
Bu soruda, özdeş iki cisim farklı uzunluktaki eğik düzlemler üzerinden 20 cm yüksekliğe çıkarılmaktadır. Şekil I’deki eğik düzlemin taban uzunluğu 40 cm, Şekil II’deki eğik düzlemin taban uzunluğu ise 60 cm’dir. Her iki durumda da cisimleri aynı yüksekliğe (20 cm) çıkardığımızdan, yerçekimi kuvvetine karşı yaptığımız iş ideal (sürtünmesiz) varsayımlarda aynı olur. Ancak daha kısa ve dik bir eğik düzlemde (I. durum) daha büyük kuvvet uygulanırken, daha uzun ve yatay eğimli düzlemde (II. durum) daha küçük bir kuvvet uygulanması beklenir.
Soruda bize verilen şıklar incelendiğinde, “I. durumda uygulanan kuvvet fazladır, her iki durumda yapılan işler aynıdır.” ifadesi (yani C şıkkı) doğru sonucu yansıtmaktadır.
1. Kavramların Tanımı ve Temel İlkeler
1.1. İş (W)
Fizikte iş, bir kuvvetin etkisiyle bir cismin konumunun değişmesi sonucu enerji aktarımını ifade eder. Matematiksel olarak en basit tanımıyla (sürtünme vb. kuvvetlerin ihmal edildiği durumda):
Burada:
- F: Uygulanan kuvvet (Newton)
- d: Cismin kuvvet doğrultusunda aldığı yol (metre)
1.2. Yerçekimine Karşı Yapılan İş
Bir cismi sabit hızla bir yüksekliğe çıkardığımızda (ivme yok, sürtünme ihmal), yerçekimine karşı yapılan iş, cismin kazandığı potansiyel enerjinin miktarına eşittir:
- m: Cismin kütlesi
- g: Yerçekimi ivmesi (Dünya için yaklaşık 9,8 m/s²)
- h: Cisim yükseltilen dikey mesafe
Her iki durumda cisim 20 cm (0,20 m) yüksekliğe çıkıyor olduğundan, sürtünme ihmal edildiğinde yapılan iş m \cdot g \cdot 0{,}20 olur ve her iki eğik düzlem için aynıdır.
2. Eğik Düzlemde Kuvvet Analizi
Eğik düzlemde, cismi sabit hızla yukarı çekerken dinamometrenin gösterdiği kuvvet, genellikle cismin ağırlık bileşenine eşittir. Bu bileşen şöyle hesaplanabilir:
- \theta: Eğik düzlemin yatayla yaptığı açı (ya da cisme etki eden ağırlık vektörünün eğik düzleme dik bileşeniyle ilgili trigonometrik açıdır)
Daha dik bir eğik düzlemde \sin\theta değeri daha büyük olacağından, kuvvet de daha büyüktür. Daha basit bir anlatımla, kısa ve dik rampa = büyük kuvvet, kısa yol; uzun ve yatay rampa = küçük kuvvet, uzun yol.
- Şekil I: 40 cm taban – 20 cm boyuna dik yükselti. Dik üçgen ilişkisine göre \sin\theta_1 = \frac{20}{40} = \frac{1}{2}, dolayısıyla \theta_1 daha büyüktür.
- Şekil II: 60 cm taban – 20 cm dik yükselti. Burada \sin\theta_2 = \frac{20}{60} = \frac{1}{3}, dolayısıyla \theta_2 daha küçüktür.
Dolayısıyla I. durumda kuvvet daha büyük, II. durumda kuvvet daha küçük olur.
3. İş Karşılaştırması
3.1. İdeal Durum (Sürtünmesiz)
Cismi aynı yüksekliğe çıkarmak için yapılan iş, cismin kazandığı potansiyel enerjidir. Her iki durumda da şu kadar iş yapılır:
Bu nedenle yapılan işler aynıdır.
3.2. Sürtünme Var mı?
Soruda sürtünme hakkında özel bir bilgi verilmemiştir. Genellikle bu tür sorularda “ideal eğik düzlem” veya “sürtünme ihmal edilmiştir” ibaresi varsayılır. Soruda açıkça belirtilmemiş olsa da standart yaklaşım, sürtünmenin ya ihmal edilmesi ya da aynı malzemeye ait sürtünme kuvvetlerinin benzer olduğu varsayımıyla her iki durumda da yapılan işin (kazandırılan potansiyel enerji) eşit oluşudur. Her ne kadar gerçek hayatta daha fazla mesafe kat edildiğinde sürtünmeden kaynaklı kayıplar artabilse de, lise düzeyi fizik sorularında çoğu zaman bu detay ihmal edilir.
4. Sorudaki Seçeneklerin Değerlendirilmesi
Soruda verilen şıklar şunlardır (özetle):
A) I. durumda uygulanan kuvvet büyük, II. durumda yapılan iş daha fazla.
B) II. durumda uygulanan kuvvet büyük, I. durumda yapılan iş daha fazla.
C) I. durumda kuvvet daha fazla, iki durumda da yapılan işler aynı.
D) II. durumda kuvvet ve yapılan iş daha fazla.
Bu fizik prensiplerine göre:
- I. durumda (kısa ve dik rampa) kuvvet büyüktür.
- Her iki durumda da yükseklik aynı ise yapılan işler eşittir.
Dolayısıyla C şıkkı doğru cevaptır.
5. Adım Adım Çözüm Özeti
- Dikey Yükseklik (h): Her iki eğik düzlemde cisim 20 cm (0,20 m) yukarı çıkarılır.
- Kuvvet Bileşeni: Eğik düzlemin açısı büyüdükçe, cismin ağırlığının eğik düzleme paralel bileşeni (çekmek için gereken kuvvet) artar. Kısa ve dik rampada bu açı büyük, dolayısıyla kuvvet fazladır.
- Toplam İş: İş = Kazanılan potansiyel enerji = m g h. Yükseklik her iki durumda da aynı olduğu için iş aynıdır.
- Sonuç: I. rampada uygulanan kuvvet daha fazla, fakat yapılan işler her iki rampada da eşit.
Aşağıdaki tabloda temel farklar özetlenmiştir:
| Özellik | Şekil I (40 cm taban) | Şekil II (60 cm taban) |
|---|---|---|
| Eğik Düzlem Uzunluğu | 40 cm | 60 cm |
| Yükseklik (Aynı) | 20 cm | 20 cm |
| Eğik Düzlem Açısı (yaklaşık) | Daha büyük (dik) | Daha küçük (yatık) |
| Dinamometrenin Gösterdiği Kuvvet | Daha büyük | Daha küçük |
| Yapılan İş (mg·h) | Aynı | Aynı |
Sonuç olarak, bu bilgiler ışığında doğru cevap:
I. durumda uygulanan kuvvet fazladır, iki durumda da yapılan işler aynıdır. (C Şıkkı)