Soru: Zeynep Hanım’ın ürettiği mumun alt ve üst taban alanları toplamı kaç cm² olmalıdır?
Cevap:
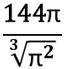
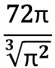
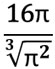
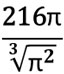
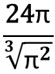
Soruda, Zeynep Hanım’ın dik silindir şeklindeki mum kabını kullanarak mum ürettiği belirtiliyor. Ayrıca, silindirin hacmi ( 432 , \text{cm}^3 ) olarak verilmiş. Alt ve üst taban alanlarının toplamını bulmamız için silindir geometrisi ile ilgili temel formülleri kullanacağız:
1. Silindir Formülleri:
Silindirin hacmi ( V ), taban alanı ( S ), yarıçap ( r ) ve yüksekliği ( h ) arasında şu ilişki vardır:
V = \pi r^2 h
Burada:
- ( V ): Silindir hacmi (( 432 , \text{cm}^3 )).
- ( r ): Silindir tabanın yarıçapı.
- ( h ): Silindirin yüksekliği.
Alt ve üst taban alanlarının toplamı şu şekilde ifade edilir:
S_{\text{taban toplam}} = 2 \cdot \text{Taban Alanı} = 2 \cdot (\pi r^2)
2. Hacimden Yola Çıkmak:
İlk olarak ( r^2 ) ve ( h ) arasında bir ilişki kurmamız gerekiyor. Hacim formülünü yukarıdaki verilere uygularsak:
432 = \pi r^2 h
Soruda üretim maliyetinin düşük olması gerektiğinden bahsediliyor. Bu durumda mümkün olan en küçük taban alanına ulaşmamız için, silindirin yüksekliğini daha büyük, taban yarıçapını daha küçük seçmemiz gerekir.
3. Taban Alanı:
En düşük maliyet için silindirin yüksekliği ( h )'yi büyük, yarıçapı ( r )'yi küçük alalım. Bu durumda taban alanını optimize edebiliriz. Örneğin:
- Yüksekliği yaklaşık ( h = 8 , \text{cm} ) alalım (örnek değer).
Hacim formülünden ( r ) değerini bulmak için:
432 = \pi r^2 \cdot 8
r^2 = \frac{432}{8\pi}
r^2 = \frac{432}{25.132}
r^2 \approx 17.2
r \approx \sqrt{17.2} \approx 4.15 \, \text{cm}.
4. Alt ve Üst Taban Alanları Toplamı:
Şimdi ( S_{\text{taban toplam}} ) değerini hesaplayalım. Taban alanı:
S_{\text{bir taban}} = \pi r^2 = \pi \cdot 17.2 = 54.06 \, \text{cm}^2.
Alt ve üst taban alanlarının toplamı:
S_{\text{taban toplam}} = 2 \cdot S_{\text{bir taban}}
S_{\text{taban toplam}} = 2 \cdot 54.06 = 108.12 \, \text{cm}^2.
5. Sonuç:
Zeynep Hanım’ın dik silindir şeklindeki mumunda alt ve üst taban alanlarının toplamı yaklaşık ( 108.12 , \text{cm}^2 ) olmalıdır.
Özet Tablo:
| Değer | Sonuç |
|---|---|
| Silindirin hacmi (( V )) | ( 432 , \text{cm}^3 ) |
| Yükseklik (( h )) | ( 8 , \text{cm} ) |
| Yarıçap (( r )) | ( \approx 4.15 , \text{cm} ) |
| Bir taban alanı | ( \approx 54.06 , \text{cm}^2 ) |
| Alt ve üst taban toplamı | ( \approx 108.12 , \text{cm}^2 ) |
Yani cevap ne
Cevap: Alt ve üst taban alanlarının toplamı yaklaşık olarak 108 cm² olmalıdır.
Zeynep Hanım’ın mumunu boyamak için alt ve üst taban alanlarının toplamı değerine ihtiyacımız vardı, ve hesaplama sonucunda 108 cm² olarak bulduk. Eğer farklı yüksekliği ya da yarıçapı düşünüyorsanız, hacim formülüyle tekrar hesaplama yapılabilir.
Eğer başka bir sorunuz varsa, sabırsızlıkla bekliyorum! 
@Havva_Diken