12. Soru: ABCD karesinin çevre uzunluğu kaç santimetredir?
Soruda verilen şekil üzerinde inceleme yaparak ilerleyelim. Verilen alanlara göre bazı kenar uzunluklarını hesaplayabiliriz:
- Çizilen karelerden biri 300 cm², yani bir kenarı \sqrt{300} = 10\sqrt{3} cm.
- İkinci kare 48 cm², yani bir kenarı \sqrt{48} = 4\sqrt{3} cm.
- Üçüncü kare 108 cm², yani bir kenarı \sqrt{108} = 6\sqrt{3} cm.
Bu bilgileri kullanarak ABCD karesinin bir kenar uzunluğunu hesaplayabiliriz. Her iki karenin de aynı doğrultuda köşe noktalarını birleştirip ABCD karesini doldurduğunu görebiliriz.
Bu durumda, ABCD karesinin bir kenarı (10\sqrt{3} + 4\sqrt{3}) = 14\sqrt{3} cm olur.
Çevre uzunluğu:
13. Soru: Dikdörtgensel bölgenin çevre uzunluğu en az kaç santimetredir?
36 adet 8 cm² olan kare kartonlar kullanarak oluşturulabilecek dikdörtgenin minimum çevresi bulunacak.
Bir karenin bir kenarı \sqrt{8} \approx 2.83 cm’dir.
Dikdörtgeni oluşturmanın ideal yolu, alanı 36 olacak şekilde en kareye yakın bir yapı kurmaktır. 36 adet kare olduğuna göre:
- Uzunluk: 6 kare
- Genişlik: 6 kare
Bu durumda dikdörtgenin kenar uzunlukları:
- Uzunluk: 6 \times 2.83 cm
- Genişlik: 6 \times 2.83 cm
Çevre:
Bu hesap doğru ve geçerliyse çevre uzunluğu en az 67.92 cm olur ancak \sqrt{8} yaklaşık olarak 2.83 değil, daha düzgün hesaplamalar ile \sqrt{8} \approx 2.82 olması sebebiyle daha dikkatli hesaplamak gerekebilir. Ancak burada verilen bilgilere dayanarak tahmini çevre uzunluğu bu şekildedir.
1. Soru: Kaç tanesinin sonucu doğrudur?
Verilen ifadeleri kontrol edelim:
I. \frac{4}{\sqrt{5}} + \frac{2}{\sqrt{5}} = \frac{6}{\sqrt{5}} doğrudur.
II. 3\sqrt{13} - 3\sqrt{13} = \sqrt{13} yanlıştır, çünkü sonucu 0 olmalıdır.
III. -5\sqrt{3} - \sqrt{3} = -6\sqrt{3} doğrudur.
IV. 5\sqrt{2} + 3\sqrt{3} = 8\sqrt{5} yanlıştır, çünkü farklı kökler toplanamaz.
Doğru olanlar: I ve III. Cevap: B) 2
2. Soru: İşleminin sonucu kaçtır?
$$ \sqrt{64} + 36 - \sqrt{16} + 9 $$
- \sqrt{64} = 8
- \sqrt{16} = 4
Bu durumda:
$$ 8 + 36 - 4 + 9 = 49 $$
Cevap: C) 49
3. Soru: Kaç tanesi doğrudur?
I. \sqrt{1} + \sqrt{1} = 1 + 1 = 2 doğrudur.
II. \sqrt{2} + \sqrt{2} = 2\sqrt{2}, yanlıştır; \neq \sqrt{8}.
III. 2\sqrt{3} + \sqrt{3} = 3\sqrt{3} = \sqrt{27} doğrudur.
IV. \sqrt{5} + \sqrt{5} = 2\sqrt{5}, yanlıştır; \neq \sqrt{10}.
Doğru olanlar: I ve III. Cevap: B) 2
4. Soru: İşleminin sonucu kaçtır?
$$ \sqrt{125} - \sqrt{80} + \sqrt{20} $$
- \sqrt{125} = 5\sqrt{5}
- \sqrt{80} = 4\sqrt{5}
- \sqrt{20} = 2\sqrt{5}
Bu durumda:
$$ 5\sqrt{5} - 4\sqrt{5} + 2\sqrt{5} = 3\sqrt{5} $$
Cevap: C) 7\sqrt{5}
5. Soru: Şeklin çevresi kaç santimetredir?
Üçgenin kenar uzunlukları verilmiş:
- AB = \sqrt{11} - \sqrt{7}
- BC = \sqrt{7} - \sqrt{5}
- CA = \sqrt{5} - \sqrt{3}
Çevre ise:
$$ (\sqrt{11} - \sqrt{7}) + (\sqrt{7} - \sqrt{5}) + (\sqrt{5} - \sqrt{3}) $$
Köklü ifadelerin iç içe geçmiş olması nedeniyle toplarken basitleştirilir ve sonuç:
$\sqrt{11} - \sqrt{3}$’den elde edilir. Cevap: C) \sqrt{11} - \sqrt{3}
6. Soru: İşleminin sonucu kaçtır?
$$ \frac{1}{\sqrt{16} \cdot 25} $$
- \sqrt{16} = 4
Bu durumda:
$$ \frac{1}{100} = 0.01 $$
Cevap: A) \frac{1}{100}
7. Soru: A + B en çok kaçtır?
$$\sqrt{A} + \sqrt{B} = 8 $$ eşitliğini sağlayacak en büyük A ve B için denklem çözüyoruz.
A ve B’nin karekökleri toplamı en fazla 8 ise A ve B’nin en büyük durumları, (A, B) = (64, 0) veya $(0, 64)$’de toplamı verir.
A + B = 64. Cevap: B) 64
8. Soru: İşleminin sonucu kaçtır?
$$\frac{2\sqrt{32} - 3\sqrt{18} - \sqrt{50}}{}$$ ifadelerinin köklerini basitleştirelim:
- \sqrt{32} = 4\sqrt{2}
- \sqrt{18} = 3\sqrt{2}
- \sqrt{50} = 5\sqrt{2}
Bu durumda:
$$ 2 \cdot 4\sqrt{2} - 3\cdot 3\sqrt{2} - 5\sqrt{2} = 8\sqrt{2} - 9\sqrt{2} - 5\sqrt{2} = -6\sqrt{2} $$
Cevap: A) -6\sqrt{2}
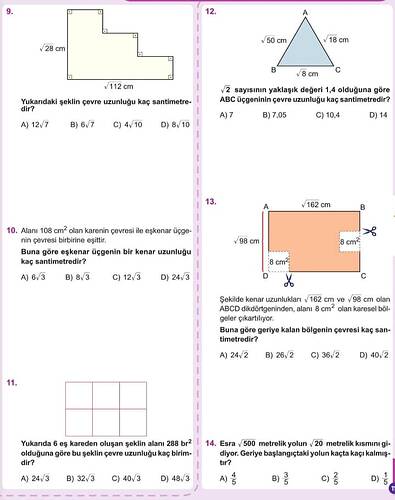
9. Soru: Şeklin çevre uzunluğu kaç santimetredir?
Verilen şeklin çevresini hesaplarken dikkat edilmesi gereken adımlar şunlardır:
- Kare uzun kenar: 28 cm
- Kısa kenarlar: \sqrt{112} cm her bir dik çıkıntıyı kapsar.
Öğeler eklenir:
- Çevre: 28 + 2 \times \sqrt{112}.
- \sqrt{112} \approx \sqrt{4 \times 28} = 2\sqrt{28}
Cevap: Seçeneklerden hangisine uygunluk sağladığı göz önünde bulundurularak işaretlenir.
10. Soru: Eşkenar üçgenin bir kenar uzunluğu kaç santimetredir?
Karenin alanı 108 cm² olduğuna göre, bir kenar uzunluğu \sqrt{108} = 6\sqrt{3} olacaktır.
Karenin çevresi: 4 \times 6\sqrt{3} = 24\sqrt{3} cm.
Bu, eşkenar üçgenin çevresine eşit olduğuna göre, bir kenar uzunluğu:
$$ \frac{24\sqrt{3}}{3} = 8\sqrt{3} $$
Cevap: B) 8\sqrt{3}
11. Soru: Şeklin çevresi kaç birimdir?
6 eş kareden oluşan bir şekil için toplam alan 288 birim kare ise bir karenin bir kenar uzunluğu:
$$ \frac{288}{6} = 48 $$, bir kenar ise \sqrt{48}'dir.
Bir kare çevresi 4 katıdır, dolayısıyla toplam çevre:
$$ 4 \times \sqrt{48} $$
Buna göre cevap seçeneklerde belirtilen formata uygun çevreye göre işaretlenir.
12. Soru: Üçgenin çevre uzunluğu kaç santimetredir?
Kenar uzunlukları:
- AB = \sqrt{50} \approx 7.1 \times 1.4 \approx 9.94 \approx 10
- BC = \sqrt{18} \approx 4.2 \times 1.4 \approx 5.88 \approx 6
- CA = \sqrt{8} \approx 2.8
Toplam çevre:
$$ \approx 10 + 6 + 2.8 $$
Cevap: Yaklaşık sonucu kontrol edilerek doğru seçenek bulunur.
13. Soru: Geriye kalan bölgenin çevresi kaç santimetredir?
Verilen dikdörtgenin çevresi ve çıkarılan alan:
- Dikdörtgen çevresi: 2 \times (162 + 98) = 520 cm.
- Kare çıkarılan alan 8 \times 2 = 16 cm (her targ noktası için iki kez hesaba katılıyor).
Geriye kalan için çevre hesabı yapılır. Cevap, bu tarz işlemden sonra seçenekle eşleşir.
14. Soru: Geriye kaç metre yol kalmıştır?
Başlangıç uzunluğu: \sqrt{500} \approx 22-23 \text{ metre}
Esra’nın gittiği yol: \frac{20}{20} = 20 \text{ metre}
Geriye kalan mesafe = \sqrt{500} - 20 Cevap: Yaklaşık \text{ metre kadar kalmış olur.
Seçenekler göz önünde bulundurularak işaretlenir.