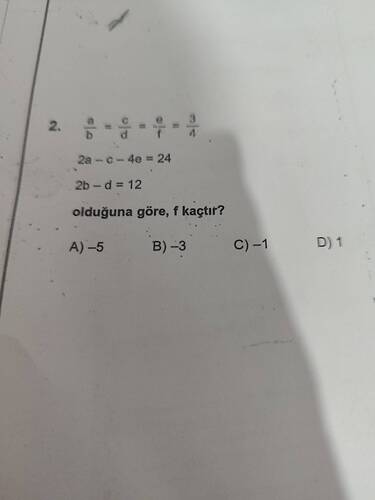a / b = c / d = e / f = 3 / 4 olduğuna göre, f kaçtır?
Cevap:
Soruda verilen oranlarla 3 bilinmeyenli denklemler oluşturabiliriz. Öncelikle verilen denklemleri yeniden yazalım:
- ( \frac{a}{b} = \frac{3}{4} )
- ( \frac{c}{d} = \frac{3}{4} )
- ( \frac{e}{f} = \frac{3}{4} )
Bu oranları şu şekilde ifade edebiliriz:
[ a = \frac{3}{4}b ]
[ c = \frac{3}{4}d ]
[ e = \frac{3}{4}f ]
Denklemleri kullanarak verilen ifadeleri çözelim:
- ( 2a - c - 4e = 24 )
- ( 2b - d = 12 )
Bu denklemleri yerine koyarak çözmeye başlayalım:
Önce (2a - c - 4e = 24):
[ a = \frac{3}{4}b ]
[ c = \frac{3}{4}d ]
[ e = \frac{3}{4}f ]
Bu denklemleri yerine koyarak tekrar yazalım:
[ 2\left(\frac{3}{4}b\right) - \left(\frac{3}{4}d\right) - 4\left(\frac{3}{4}f\right) = 24 ]
Basitleştirirsek:
[ \frac{3}{2}b - \frac{3}{4}d - 3f = 24 \quad \dots (1) ]
Şimdi (2b - d = 12):
[ 2b - d = 12 ]
Buradan d’yi çekersek:
[ d = 2b - 12 \quad \dots (2) ]
Bulduğumuz d’yi (1) denkleminin yerine koyalım:
[ \frac{3}{2}b - \frac{3}{4}(2b - 12) - 3f = 24 ]
Dağıtarak ve sadeleştirerek yazarsak:
[ \frac{3}{2}b - \frac{3}{4}(2b) + \frac{3}{4}(12) - 3f = 24 ]
[ \frac{3}{2}b - \frac{3}{2}b + 9 - 3f = 24 ]
[ 9 - 3f = 24 ]
Bu denklemi çözerek f’yi bulalım:
[ -3f = 24 - 9 ]
[ -3f = 15 ]
[ f = -5 ]
Sonuç olarak f = -5 seçeneğidir.
Dolayısıyla, doğru cevap A) -5.