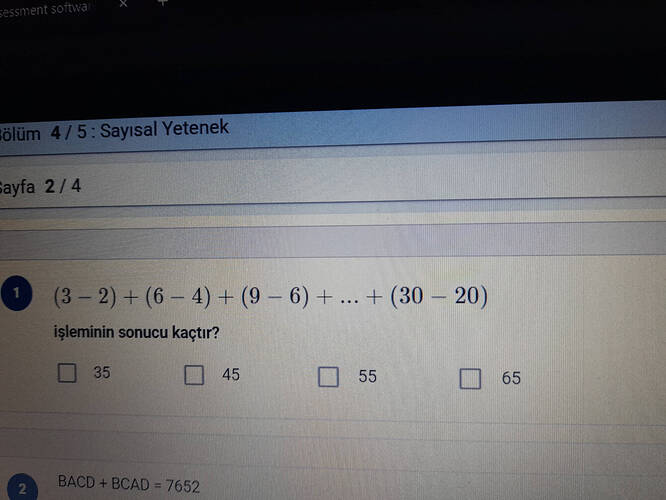
Görselde verilen işlemi çözelim:
(3 - 2) + (6 - 4) + (9 - 6) + \ldots + (30 - 20)
Bu işlemdeki her parantez içindeki ifadeyi tek tek çözelim ve sonuçları toplayalım:
- (3 - 2 = 1)
- (6 - 4 = 2)
- (9 - 6 = 3)
- …
- (30 - 20 = 10)
Bu şekilde, bu işlemlerle bir dizi oluşturulmuş durumda: (1, 2, 3, \ldots, 10).
Bu bir aritmetik dizidir ve tüm terimlerin toplamı bulunabilir. İlk terim (a_1 = 1), son terim (a_n = 10), ve bu dizinin terim sayısı:
Dizinin ortak farkı (d = 1).
Her iki uçtaki terimleri toplayıp, toplam terim sayısını bulmak için aritmetik dizinin formülünü kullanarak, son terime kadar kaç adım olduğunu bulabiliriz. Yani,
Dizi (1, 2, 3, \ldots, 10) şeklindedir ve 10 adet terim olduğu açıktır.
Toplam:
S_n = \frac{n}{2} \times (a_1 + a_n) = \frac{10}{2} \times (1 + 10) = 5 \times 11 = 55
Sonuç olarak işlem sonucu 55’tir.