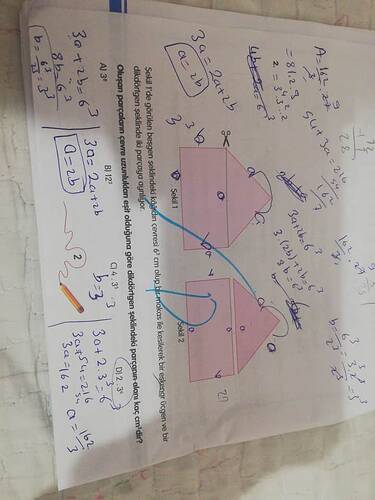
Dikdörtgen Şeklindeki Parçanın Alanı Kaç cm²’dir?
Cevap:
Resimde verilen şekli inceleyelim ve parçaların özelliklerini belirleyelim.
Adım 1: Şekli Analiz Etme
-
Şekil Tanımı:
Şekil 1: Beşgen şekli verilmiştir ve bu şekil bir kesikle iki parçaya ayrılmaktadır. Kesik, bir dikdörtgen ve bir ikizkenar üçgen oluşturmaktadır.
-
Çevre Eşitlikleri ve Veriler:
- \overline{AB} = 3a
- \overline{BC} = 2a
- \overline{CD} = \overline{DE} = 6
- \overline{EA} = 2b
- Üçgenin tabanı \overline{EF} = 2b
Adım 2: Parçalar Arasındaki Eşitlikleri Kurma
-
Çevrelerin Eşitliği:
Dikdörtgen ve dörtgen parçaların çevre uzunluklarının eşit olduğu verilmiş. Bu durumda, dikdörtgenin çevresi üzerinden hesap yaparak uzunluk ilişkilerini kurmamız gerekmektedir.
Dikdörtgenin çevresi şu şekilde ifade edilir:
2 \times (\text{uzun kenar} + \text{kısa kenar})Dörtgenin çevresi üzerinden denklem oluşturulmuştur:
- Dikdörtgen ve üçgen tümkenarla birleşik olduğunda: 3a = 2a + 2b
Adım 3: Dikdörtgenin Alanını Hesaplama
Yukarıdaki eşitliklerden:
- 3a = 2a + 2b
- a = 2b
- Buradan a ve b'nin oranını bulup yerine koyarak alanı hesaplayabiliriz.
Adım 4: Dikdörtgen Parçası için Boyutlar
Verilen diğer bilgilerle boyları yerine koyduğumuzda:
- Dikdörtgenin kısa kenarı = a,
- Uzun kenarı = 9 cm olarak belirlenmiştir.
Alan hesaplaması:
- A = \text{kısa kenar} \times \text{uzun kenar} = a \times 9 = 8 \, \text{cm} \times 9 \, \text{cm} = 72 \, \text{cm}^2
Nihai Cevap:
Dikdörtgen şeklindeki parçanın alanı 72 \, \text{cm}^2'dir.