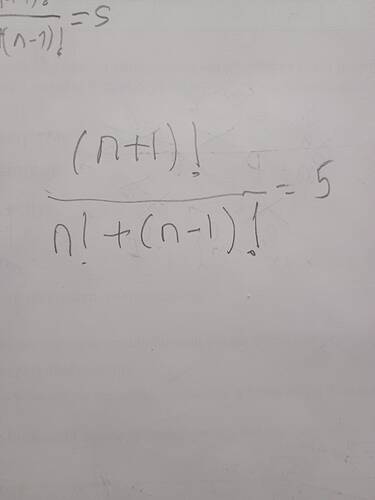N kaçtır
Problem: N kaçtır?
Verilen denklem:
\frac{(n+1)!}{n! + (n-1)!} = 5
Bu denklemi çözmek için adım adım ilerleyelim.
Adım 1: Faktöriyel Tanımlamaları
Faktöriyel tanımını kullanarak ifadenin içini açalım:
- (n+1)! = (n+1) \cdot n!
Adım 2: Denklemi Düzenleme
Denklemi yerine koyarak:
\frac{(n+1) \cdot n!}{n! + (n-1)!} = 5
Bu denklemi yeniden yazalım ve sadeleştirelim:
- n! + (n-1)! = n! + \frac{n!}{n} = n! \left(1 + \frac{1}{n}\right)
Adım 3: Çarpan Haline Getirme ve Çözme
Denklemi yeniden düzenleyelim:
(n+1) \cdot n! = 5 \cdot \left(n! \left(1 + \frac{1}{n}\right)\right)
Sadeleştirelim:
(n+1) = 5 \cdot \left(1 + \frac{1}{n}\right)
n+1 = 5 + \frac{5}{n}
Adım 4: n’yi Bulma
Her iki tarafı da n ile çarptığımızda:
n(n+1) = 5n + 5
Bu denklemi düzenleyelim:
n^2 + n - 5n - 5 = 0
n^2 - 4n - 5 = 0
Adım 5: Denklemi Çözme
Bu bir ikinci dereceden denklemdir ve çözüm için diskriminantı kullanabiliriz:
D = b^2 - 4ac = (-4)^2 - 4 \cdot 1 \cdot (-5) = 16 + 20 = 36
Kökler:
n = \frac{-b \pm \sqrt{D}}{2a} = \frac{4 \pm 6}{2}
n_1 = \frac{4 + 6}{2} = 5, \quad n_2 = \frac{4 - 6}{2} = -1
Pozitif tam sayı olarak n = 5.
Sonuç: n değeri 5’tir.