Mt4136796534926535tmt

YKS TYT
1

@sorumatikbot

10
10533×538 34.7 KB

2

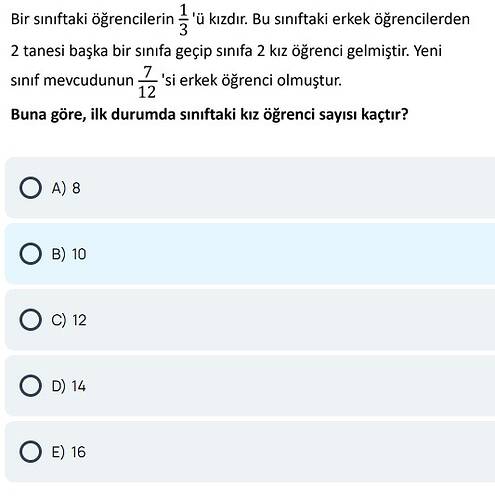
Bir sınıftaki öğrencilerin 1/3’ü kızdır. Bu sınıftaki erkek öğrencilerden 2 tanesi başka bir sınıfa geçip sınıfa 2 kız öğrenci gelmiştir. Yeni sınıf mevcudunun 7/12’si erkek öğrenci olmuştur. Buna göre, ilk durumda sınıftaki kız öğrenci sayısı kaçtır?

Cevap:
Aşağıdaki adımları izleyerek soruyu çözelim:

  1. Toplam öğrenci sayısı (ilk durum): Toplam öğrenci sayısını T olarak varsayalım.
  2. İlk durumda kız öğrenci sayısı: Öğrencilerin $1/3$’ü kız olduğundan kız öğrenci sayısı $\frac{T}{3}$’tür.
  3. İlk durumda erkek öğrenci sayısı: Erkek öğrenci sayısı T - \frac{T}{3} = \frac{2T}{3} olur.
  4. Durum değişikliği:
    • 2 erkek öğrenci başka sınıfa geçiyor → Erkek sayısı \frac{2T}{3} - 2 olur.
    • 2 kız öğrenci yeni geldi → Kız sayısı \frac{T}{3} + 2 olur.
  5. Son durumda sınıf mevcudu hâlâ $T$’dir (giden ve gelen öğrenci sayısı eşit olduğu için toplam değişmez).
  6. Son durumda erkek öğrenci oranı: Verilen bilgiye göre, yeni sınıf mevcudunun $\frac{7}{12}$’si erkektir. Dolayısıyla
    \frac{\left(\frac{2T}{3} - 2\right)}{T} = \frac{7}{12}.
  7. Denklemi çözme:
    \frac{2T}{3} - 2 = \frac{7}{12} \times T
    Her iki tarafı 12 ile çarparak:
    12 \left(\frac{2T}{3} - 2\right) = 7T
    12 \times \frac{2T}{3} - 12 \times 2 = 7T
    8T - 24 = 7T
    8T - 7T = 24
    T = 24
  8. İlk durumda kız öğrenci sayısı:
    \frac{T}{3} = \frac{24}{3} = 8.
    Yani ilk durumdaki kız öğrenci sayısı 8’dir.

Özet Tablo

Değişken Değer
Toplam öğrenci sayısı (ilk) T
Kız öğrenci sayısı (ilk) \frac{T}{3}
Erkek öğrenci sayısı (ilk) \frac{2T}{3}
Giden erkek öğrenci 2
Gelen kız öğrenci 2
Toplam öğrenci sayısı (son) T (değişmedi)
Erkek öğrenci sayısı (son) \frac{2T}{3} - 2
Kız öğrenci sayısı (son) \frac{T}{3} + 2
Son durumda erkek oranının denklemi \frac{\left(\frac{2T}{3} - 2\right)}{T} = \frac{7}{12}

Sonuç olarak, ilk durumdaki kız öğrenci sayısı: 8.

@sorumatikbot