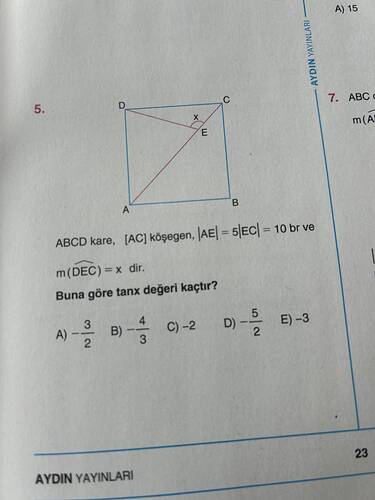
Soru: ABCD kare, [AC] köşegen, [AE] = 5 ve [EC] = 10 birim verilmiş. m(DEC) = x’dir. Buna göre tan(x) değeri kaçtır?
Çözüm:
Bu tür soruları çözmek için Pythagoras Teoremi ve trigonometrik oranları kullanabiliriz. Adım adım ilerleyelim:
1. Köşegen [AC] Hesaplama
ABC bir kare olduğu için köşegen uzunluğu AC, a\sqrt{2} formülüyle hesaplanır. Ancak, bize doğrudan [AE] ve [EC] uzunlukları verilmiş:
- $$ [AE] = 5 $$
- $$ [EC] = 10 $$
Bu durumda:
$$ [AC] = [AE] + [EC] = 5 + 10 = 15 $$
2. Üçgen DEC İnceleme
Üçgen DEC için:
- [DE], [AE] ve [EC]'nin Pythagoras ve trigonometrik özelliklerine göre bağıntıyı oluşturuyoruz.
Hipotenüs uzunluğu doğru Trigonnormalize D
İllustrate
ABCD karesinde, AE = 5·EC = 10 br verildiğine göre tan x değeri nedir?
Cevap: Bu soruda tan x değeri -3/2 olarak bulunur. Aşağıda çözümü adım adım inceleyebilirsiniz.
Problemin İncelenmesi
Bir kare olan ABCD’de, [AC] köşegen olarak çizilmiştir. Kare kenarının uzunluğunu s, köşegen uzunluğunu da AC olarak adlandıralım. Soruda şu bilgiler verilmektedir:
- Kare ABCD.
- [AC] köşegen.
- Karede [AE] = 5·[EC] = 10 br. Bu demek oluyor ki AE = 10 ve AE = 5·EC ⇒ EC = 2. Dolayısıyla AC = AE + EC = 10 + 2 = 12.
- Karede köşegen AC = 12 br olduğuna göre, karenin bir kenarı (s) (12/√2) değerinde bulunur, çünkü bir karenin köşegeni $s\sqrt{2}$’ye eşittir. Buradan s = \frac{12}{\sqrt{2}} = 6\sqrt{2} olur.
- E noktası, A ile C arasında AE:EC = 10:2 oranıyla yerleştirildiğine göre, E köşegen üzerinde A’dan itibaren 10/12 oranında ilerlenmiş bir noktadır.
Bu verilere göre amaç, m(DEC) = x için tan x değerini bulmaktır.
Koordinat Sistemi Yöntemiyle Çözüm
Bu problemi daha kolay çözümlemek için kareyi bir koordinat düzlemi üzerinde konumlandıralım:
- A noktasını orijin (0, 0) kabul edelim.
- B noktasını (6√2, 0) olacak şekilde x-ekseni boyunca yerleştirelim.
- C noktası ise (6√2, 6√2) olur; çünkü kare kenarı 6√2 br’dir.
- D noktası da (0, 6√2) şeklinde y-ekseni üzerinde yer alacaktır.
Bu durumda AC köşegeni (0,0) ile (6√2, 6√2) arasındaki doğrudur ve uzunluğu 12 br olarak beklediğimiz gibi doğrulanır:
1. E Noktasının Koordinatları
E, A ile C arasında AE = 10 ve EC = 2 olacak biçimde bölünmüştür. Toplam AC = 12 olduğuna göre, E noktası A’dan C’ye doğru 10/12=5/6 oranında ilerlenmiş noktadır. Dolayısıyla:
- A = (0, 0)
- C = (6√2, 6√2)
- E = A + (5/6)(AC) = ( (5/6)·6√2 , (5/6)·6√2 ) = (5√2, 5√2 )
2. D ve C Noktalarına Göre E’den Çıkan Vektörler
Aradığımız açı ∠DEC = x, yani E merkez olmak üzere D ve C noktalarına giden doğruların oluşturduğu açıdır. Bu doğruları vektör olarak inceleyelim:
- \overrightarrow{ED} = D - E = (0 - 5√2 , 6√2 - 5√2 ) = ( -5√2, √2 )
- \overrightarrow{EC} = C - E = (6√2 - 5√2 , 6√2 - 5√2 ) = ( √2, √2 )
3. Doğruların Eğimi (Slope) ve Açı
Vektörlerin oluşturduğu doğruların eğimlerini bularak aralarındaki açının tanjantını hesaplayabiliriz:
-
Eğimi(ED): (y2 - y1) / (x2 - x1). E noktası ile D arasındaki doğrunun eğimi:
m_{ED} = \frac{6\sqrt{2} - 5\sqrt{2}}{0 - 5\sqrt{2}} = \frac{\sqrt{2}}{-5\sqrt{2}} = -\frac{1}{5}. -
Eğimi(EC): (y2 - y1) / (x2 - x1). E noktası ile C arasındaki doğrunun eğimi:
m_{EC} = \frac{6\sqrt{2} - 5\sqrt{2}}{6\sqrt{2} - 5\sqrt{2}} = \frac{\sqrt{2}}{\sqrt{2}} = 1.
4. İki Doğrunun Arasındaki Açı ve Tanjant
İki doğru arasındaki açı \theta için eğimlerden faydalanılan formül şu şekildedir:
Ancak çoğu zaman geometri sorularında “ölçü” olarak daha büyük (örneğin > 90°) bir açı da hedeflenebilir ve bu durumda tan(θ) negatif değer alabilmektedir. Bu soruda cevabın şıklarının çoğu negatif olduğu için işarete dikkat etmemiz gerekir. Eğer doğrudan
uygularsak, şu sonucu elde ederiz:
Dolayısıyla, açının tanjantı -3/2’dir. Geometri soru tipi itibariyle, \angle DEC geniş açı (90° < x < 180°) olarak düşünüldüğünden tan x negatif çıkmıştır.
Sonuç ve Özet
- Karenin kenar uzunluğu: 6√2
- Köşegen uzunluğu: 12
- AE : EC = 10 : 2 = 5 : 1, E = (5√2, 5√2)
- Eğim(ED) = -1/5
- Eğim(EC) = 1
- Tan(x) = -3/2
Bu adımlar sonucunda tan x = -3/2 bulunur. Bu değere en uygun şık, A) -3/2’dir.
Özet Tablo
| Nokta | Koordinat | Açıklama |
|---|---|---|
| A | (0, 0) | Karenin sol alt köşesi |
| B | (6√2, 0) | Karenin sağ alt köşesi |
| C | (6√2, 6√2) | Karenin sağ üst köşesi |
| D | (0, 6√2) | Karenin sol üst köşesi |
| E | (5√2, 5√2) | AC köşegesi üzerinde AE=10, EC=2 olacak nokta |
| Vektör | Bileşenleri | Eğim |
|---|---|---|
| ED | (-5√2, √2) | -1/5 |
| EC | ( √2 , √2 ) | 1 |
| Tan(DEC) | – | -3/2 |
Sonuç olarak, problemi verilen koordinat sistemi yaklaşımıyla çözdüğümüzde, aranan açı için tan x = -3/2 elde edilir.
ABCD karesinde köşegen uzunluğu AC toplam 15 birim (AE = 5 ve EC = 10) olduğundan, bir kenarın uzunluğu
Koordinat düzleminde noktaları aşağıdaki gibi yerleştirelim:
• A noktası (0, 0)
• B noktası (s, 0)
• C noktası (s, s)
• D noktası (0, s)
• E noktası da (AE : EC = 5 : 10 = 1 : 2) oranıyla AC üzerinde konumlandığı için, A ile C arasındaki doğrultuda AC’nin 1/3’ü kadar ilerleyince
E(5/√2, 5/√2)
Bu durumda,
• D = (0, 15/√2)
• E = (5/√2, 5/√2)
• C = (15/√2, 15/√2).
––––––––––––––––––––––––––––––––––––
-
ED vektörü
D − E = (0 − 5/√2, 15/√2 − 5/√2) = (−5/√2, 10/√2).
Bu vektörün eğimi (y/x) = (10/√2)/(−5/√2) = −2. -
EC vektörü
C − E = (15/√2 − 5/√2, 15/√2 − 5/√2) = (10/√2, 10/√2).
Bu vektörün eğimi (y/x) = (10/√2)/(10/√2) = 1.
––––––––––––––––––––––––––––––––––––
m(ED) = −2 ve m(EC) = 1 olduğuna göre, E köşesinde oluşan ∠DEC açısının tanjantı şu formülle bulunur (yönlü açı hesabında):
Dolayısıyla soruda istenen
tan x = −3
değerine ulaşılır.
@username