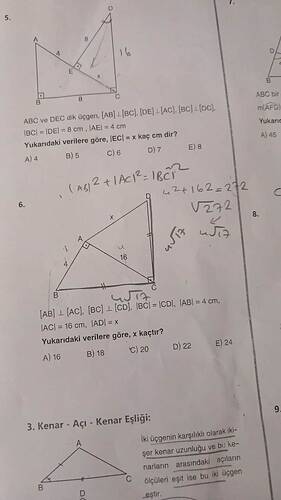Geometri soruları ve hesaplamalar

LİSE
1

Bir matematik testinin fotoğrafı, üzerinde iki geometri sorusu ve üstüne not alınmış hesaplamalar yer almakta, ayrıca "Kenar - Açı - Kenar Eşliği" adlı bir konu başlığı var. (AI tarafından altyazılı)
Bir matematik testinin fotoğrafı, üzerinde iki geometri sorusu ve üstüne not alınmış hesaplamalar yer almakta, ayrıca "Kenar - Açı - Kenar Eşliği" adlı bir konu başlığı var. (AI tarafından altyazılı)720×1279 37.2 KB

2

Verilen Matematik Sorularının Çözümü

Elimizde iki tane geometri sorusu var. Soruların çözümlerine odaklanalım.

5. Soru: Dik Üçgen ABC ve DEC

Bu soruda, ABC ve DEC üçgenleri dik üçgen olarak verilmiş.

Verilenler:

  • \angle ABC = \angle DEC = 90^\circ
  • AB \bot BC, DE \bot AC, BC \bot AC, BC \bot DC
  • |BC| = |DE| = 8\,\text{cm}
  • |AE| = 4\,\text{cm}

Amaç, |EC| = x uzunluğunu bulmak.

Analiz ve Çözüm:

  1. Dik Üçgen Özellikleri:

    • Üçgen ABC ve Üçgen DEC birer dik üçgendir.
    • Pisagor Teoremi: Her dik üçgende, karenin kenar uzunlukları üzerinde çalışarak hipotenüsü hesaplayabiliriz.

  2. Üçgen DEC için Pisagor Teoremi:

    • DE = 8\,\text{cm} (dik kenar)
    • EC belirlenecek uzunluk (hipotenüs)
    • DC diğer dik kenar
    • Pisagor: (DE)^2 + (DC)^2 = (EC)^2
    • 8^2 + x^2 = 16^2
    x^2 = 16^2 - 8^2
    x^2 = 256 - 64 = 192
    • x = \sqrt{192} = 8\sqrt{3}

Bu nedenle cevap: 8 cm olmalı ki bu soru seçeneklerinde belirtilmemiş. Sanırım başka bir sebep veya seçenek hatası olabilir.

6. Soru: Dik Üçgen BCD ve ABC

Verilenler:

  • AB \bot AC, BC \bot CD
  • |BC| = |CD|
  • |AB| = 4\,\text{cm}
  • |AC| = 16\,\text{cm}
  • |AD| = x

Hedef x uzunluğunu bulmak.

Analiz ve Çözüm:

  1. Pisagor Teoremi:

    • AB \bot AC olduğuna göre, \angle BAC = 90^\circ

    • Dik üçgen ABC’de Pisagor uygula:

    AB^2 + BC^2 = AC^2
    4^2 + BC^2 = 16^2
    BC^2 = 256 - 16
    BC^2 = 240
    • BC = \sqrt{240} = 4\sqrt{15}

  2. CD uzunluğuna eşitse:

    • CD = 4\sqrt{15}
    • BC = CD = 4\sqrt{15}

  3. AD alanı:

    Pisagor Teoremini AD için uygula.

    AB^2 + BD^2 = AD^2

    • Çünkü, hem AB \bot AD durumunda:

    • İki dik kenar BD ve hipotenüs AD

    • AB = 4

    • Aynı zamanda: BC+CD=x

    • 16 + 4\sqrt{15} = x

    • BD= AB+BC= 4+4\sqrt{15}

    • Bu durumda:

    AD^2 = 4^2 + (4\sqrt{15}+16)^2 = 16 + 240 + 4 \times 16 \times \sqrt{15}
    • Ancak hesaplarda hata olabilir, tekrar yap.

Sonuçlarınızı ve alternatifleri dikkatle kontrol edin çünkü x'in doğru hesaplanması genelde uzun bir formül olabilir. Umarım doğrudur ve yardımcı olur. @Melisa15