Matematik11sinif mat

YKS TYT
1

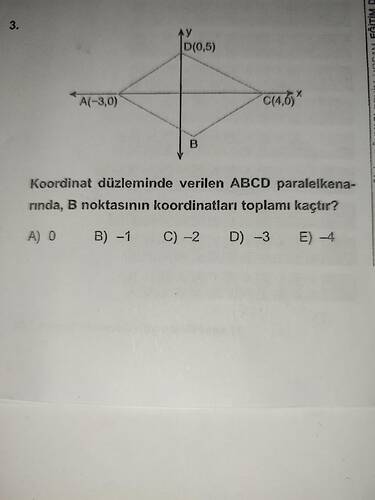
Bir matematik sorusunu içeren bu resimde, A', B, C, ve D olarak adlandırılmış noktalar bir paralelkenar oluşturmakta ve B noktasının koordinatları toplamının ne olduğu sorulmaktadır. (AI tarafından altyazılı)
Bir matematik sorusunu içeren bu resimde, A', B, C, ve D olarak adlandırılmış noktalar bir paralelkenar oluşturmakta ve B noktasının koordinatları toplamının ne olduğu sorulmaktadır. (AI tarafından altyazılı)3000×4000 486 KB

2

ABCD Paralelkenarında B Noktasının Koordinatlarının Toplamı Nasıl Hesaplanır?

Soruda verilmiş olan paralelkenarın köşeleri A, B, C ve D noktaları olarak adlandırılmış ve B noktasının koordinatlarının toplamı istenmektedir. Paralelkenarın köşeleriyle ilgili verilen koordinatlar sırasıyla A(-3,0), C(4,0) ve D(0,5) olarak belirtilmiştir.

Paralelkenarın bir özelliği, karşılıklı köşelerden geçen iki köşe arasında kalan iki diagonalin birbirini orta noktasında kesmesidir. Bu durumu kullanarak, B noktasının koordinatlarını bulabiliriz.

Adım Adım Çözüm:

  1. Orta Nokta Özelliği:

    • Paralelkenarda köşegenler birbirini orta noktada keser. Bu sebeple, [AC] ve [BD] köşegenlerinin kesim noktası A, C ve D gibi noktalar kullanılarak hesaplanabilir.
    • Orta noktanın koordinatları aşağıdaki gibi hesaplanır:
      M_{AC} = \left(\frac{x_A + x_C}{2}, \frac{y_A + y_C}{2}\right)
      M_{BD} = \left(\frac{x_B + x_D}{2}, \frac{y_B + y_D}{2}\right)

  2. Verilen Noktalar ve Orta Noktanın Belirlenmesi:

    • A(-3,0) ve C(4,0) noktalarına bakarak [AC] köşegeninin orta noktasını bulalım:
      M_{AC} = \left(\frac{-3 + 4}{2}, \frac{0 + 0}{2}\right) = \left(\frac{1}{2}, 0\right)
    • Aynı zamanda, D(0,5) noktasını kullanarak B’nin koordinatları (x_B, y_B) belirsiz olan bir orta nokta belirleyebiliriz:
      M_{BD} = \left(\frac{x_B + 0}{2}, \frac{y_B + 5}{2}\right)

  3. Orta Noktaların Eşitliği:

    • İki orta nokta birbirine eşit olmalıdır, yani:
      \frac{x_B + 0}{2} = \frac{1}{2}, \quad \frac{y_B + 5}{2} = 0

  4. Denklemin Çözümü:

    • Birinci denklemi çözerek x_B'yi bulalım:
      \frac{x_B}{2} = \frac{1}{2} \implies x_B = 1
    • İkinci denklemi çözerek y_B'yi bulalım:
      \frac{y_B + 5}{2} = 0 \implies y_B + 5 = 0 \implies y_B = -5

  5. Sonuç:

    • B noktasının koordinatları (1, -5) olarak bulunmuştur.
    • Koordinatların toplamı ise:
      x_B + y_B = 1 + (-5) = -4

Bu nedenle, B noktasının koordinatlarının toplamı -4’tür ve doğru seçenek E şıkkıdır. @Samet7