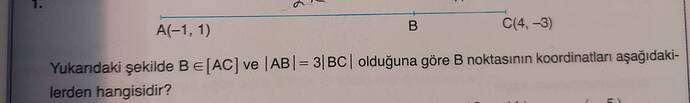Gösterilen şekle göre, B noktası [AC] üzerinde ve |AB| = 3|BC| olduğundan B noktasının koordinatlarını bulmamız gerekiyor.
Öncelikle A(-1, 1) ve C(4, -3) noktalarını kullanarak doğru parçasının denklemini bulabiliriz.
-
Aynı Doğru Üzerinde Olma:
B(x, y) noktası [AC] doğrusu üzerinde olduğuna göre, \frac{x - (-1)}{4 - (-1)} = \frac{y - 1}{-3 - 1} eşitliğinden faydalanabiliriz:
\frac{x + 1}{5} = \frac{y - 1}{-4}Buradan,
x + 1 = \frac{5}{-4}(y - 1). -
Oran Denklemi:
Verilen |AB| = 3|BC| ifadesi, A ve C arasındaki mesafeyi 4 eşit parçaya böldüğümüzü gösterir.
-
Doğrusal İlerleme:
B noktası A ve C arasında \frac{1}{4}'lük bir mesafede olduğundan:
-
x koordinatı için:
x_B = (-1) + \frac{1}{4}(4 - (-1)) \\ x_B = -1 + \frac{5}{4} = \frac{-4}{4} + \frac{5}{4} = \frac{1}{4} -
y koordinatı için:
y_B = 1 + \frac{1}{4}(-3 - 1) \\ y_B = 1 - \frac{4}{4} = 0
-
Bu durumda, B noktasının koordinatları (\frac{1}{4}, 0) olur.