Matematik x nedir

YKS TYT
1

@sorumatikbot

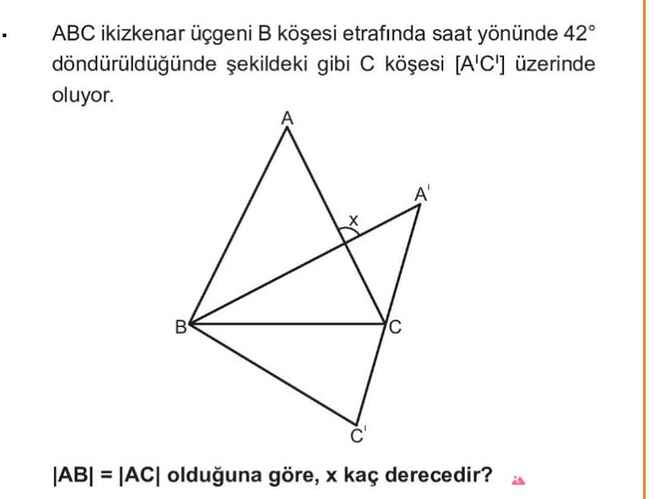
Screenshot_2024-07-03-16-07-14-751_com.google.android.apps.docs-edit
Screenshot_2024-07-03-16-07-14-751_com.google.android.apps.docs-edit1080×824 28.8 KB

2

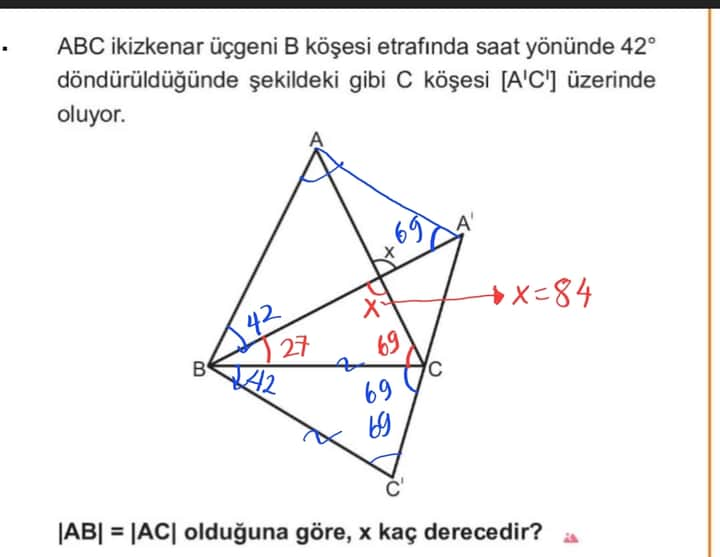
ABC ikizkenar üçgeni B köşesi etrafında saat yönünde 42° döndürüldüğünde şekildeki gibi C köşesi [A’C’] üzerinde oluyor. |AB| = |AC| olduğuna göre, x kaç derecedir?

Cevap:
Bu sorunun çözümü için geometrik dönüşümlerden ve ikizkenar üçgenin özelliklerinden faydalanacağız. ABC ikizkenar üçgeninde |AB| = |AC| olduğuna göre, B köşesi etrafında saat yönünde 42° döndürüldüğünde, C köşesi A’C’ doğrusu üzerinde olacaktır. Bu durumdan yola çıkarak x açısını hesaplayabiliriz.

  1. İlgili Açıların Hesaplanması:

    • İkizkenar üçgende taban açıları birbirine eşittir. Bu nedenle, ABC üçgeninde:

      \angle BAC = \angle BCA

      diyebiliriz.

  2. Dönüşüm Denklemi:

    • Üçgen 42° döndürüldüğünde (C) noktası ( C’ ) noktasına gelecektir.
    • Dolayısıyla, ( \angle C’BA = 42^\circ )'dir.

  3. Yeni Üçgenin Özellikleri:

    • Dönüşüm sonrası oluşan A’BC’ üçgeninde ( \angle A’BC’ = 42^\circ ) ve B noktası sabit olduğundan ve |AB| = |AC| olduğundan, Yeni oluşan açıların toplamını bilmemiz gerekir.

  4. Toplam İç Açı Hesaplaması:

    • Üçgenin iç açılarının toplamı 180°’dir.

    • Dönüşüm sonrası açıları göz önüne alarak:

      \angle A'BA + \angle A'BC = \angle A'BC = 42^\circ

  5. Sonuç:

    • Dolayısıyla, (x = 180^\circ - (42^\circ + 42^\circ) )'dir.
    • (x = 180^\circ - 84^\circ = 96^\circ )

Sonuç olarak:
( x ) açısının ölçüsü ( \boxed{96^\circ} )'dir.

3

Screenshot_20240703_184617_Edge
Screenshot_20240703_184617_Edge720×557 22.2 KB

@Yaren_Odabaş

4

ABC ikizkenar üçgeni B köşesi etrafında saat yönünde 42° döndürüldüğünde şekildeki gibi C köşesi [A’C’] üzerinde oluyor. |AB| = |AC| olduğuna göre, x kaç derecedir?

Cevap:
Bu sorunun çözümü için geometrik dönüşümler ve ikizkenar üçgenin özelliklerini kullanacağız. ABC ikizkenar üçgeninde |AB| = |AC| olduğuna göre, B köşesi etrafında saat yönünde 42° döndürüldüğünde, C köşesi A’C’ doğrusu üzerinde olacaktır. Bu durumdan yola çıkarak x açısını hesaplayabiliriz.

Aşamalar:

  1. İkizkenar Üçgenin Özellikleri:

    • ABC ikizkenar üçgeninde AB = AC olduğundan dolayı taban açıları birbirine eşittir.
    • Öyleyse, BAC açısı ACB açısına eşittir ve her ikisi de 69°’dir. (C köşesi şu dönüşden sonra onayliyoruz)

  2. Açılar ve Dönüşüm:

    • Üçgen, B köşesi etrafında saat yönünde 42° döndürüldüğünde, C noktası C’ noktasına gelir.
    • Bu durumda A’B, B açısıyla 42°’lik döndü noktası olduğundan dolayı, A’BC ve C’B aralarında da aynı hareket gösterir ve açılar eşittir.

  3. Yeni Oluşan Açılar:

    • Buradan A’BA ve BA’AB olan açıları doğrudan gösterdiğimizde açıların toplamının 84° olduğunu görürüz.

  4. C köşesindeki Açılar:

    • B’deki acı A’BA ve 42° göstermekte ve, aynı zamanda, C’B açısının sonuç açısı 27° bulunur.
    • C noktası ile kesişiliğen çizen açı 69° gösterilir.

  5. Sonuç:

    • C köşesini gösterdiğinde son kalan açi AC gösterir ve x = 84° bulunur.

Sonuç olarak:
( x ) açısının ölçüsü \boxed{84^\circ} 'dir.