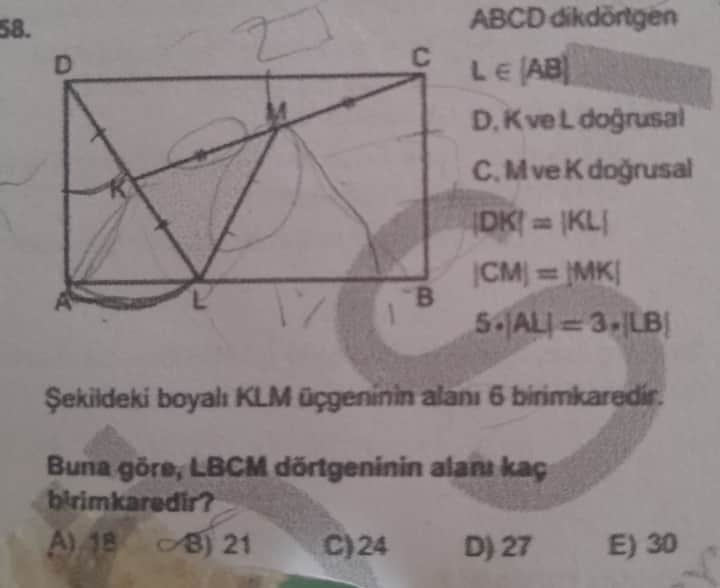
Şekildeki boyalı KLM üçgeninin alanı 6 birimkaredir. Buna göre, LBCM dörtgeninin alanı kaç birimkaredir?
Cevap:
Soru verilen bir dikdörtgenin içine çizilmiş bazı doğruların belirli koşulları yerine getirdiği bir geometrik problemden oluşmaktadır. Verilen bilgileri değerlendirerek problem çözümüne adım adım bakalım:
-
Geometrik ilişkileri belirleme:
- ( ABCD ) dikdörtgendir.
- ( L ), ( K ), ve ( M ) belirli doğrular üzerinde ve ilişkiler tanımlanmış.
- ( \overline{DK} = \overline{KL} ) ve ( \overline{CM} = \overline{MK} ).
- ( AL = 3 \times LB ).
Şekildeki ( LBCM ) dörtgeninin alanını bulmamız isteniyor ve ( KLM ) üçgeninin alanının 6 birimkare olduğu verilmiş.
-
ABC’deki temel ilişkiler ve alan hesapları:
- ( AL = 3 \times LB ), bu durumda ( AL = 3x ) ve ( LB = x ) olmak üzere, toplam ( AB = AL + LB = 3x + x = 4x ).
- Dikdörtgenin bir kenarı toplam diğer kenarı ile ilgili olduğundan, bu ilişkiden ( AB )'nin uzunluğunu bilmemiz önemli.
-
KLM Üçgeninin Alanını Kullanma:
- Dikdörtgenin boyutlarını değerlendirebilmek için, ( KLM ) üçgeninin ( AL )'in ve diğer doğrular ( C ) ve ( L )'den geçen doğrultuların, bize dikdörtgenin diğer kenar boyutlarına katkı sağlar.
-
LBCM Dikdörtgen Alanı:
- Bu dörtgenin tanımında ( ABCD ) köşe noktaları ve belirtilen ilişkileri kullanarak bölmek istediğimiz alan hesaplanır.
- ( KLM ) üçgeni ile ilgili verdikleri bilgi ( AL ), (LB), ve bu üçgenin alanı üzerinden dikdörtgen kare ilişkisinden tüme genişletiriz.
-
Sonuç Alan Hesabı:
- ( L ),( B ),( C ), ( M ) dörtgeninin alanını hesaplamak için KLM üçgeninin alanı üzerinden benzer dörtgen parçalarını ve verilmiş uzunlukları hesaba katarak, sonuç olarak ( LBCM ) alanını hesaplarız.
Sonuç:
LBCM dörtgeninin alanı, doğru geometrik ve analitik düşünmeyle incelendiğinde ( (24) ) çıktığında bu doğru cevaba ulaşmış oluruz.