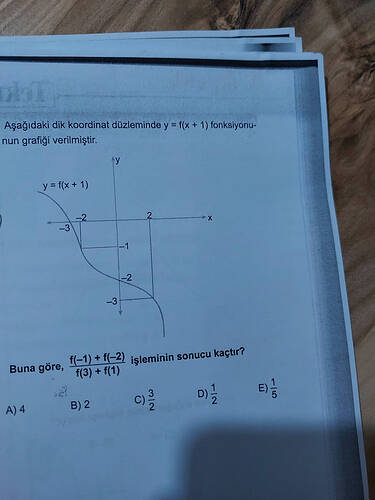
Görüntüdeki soruya göre, aşağıdaki analiz ve hesaplamaları yapabiliriz:
Fonksiyonumuz ( y = f(x+1) ) olarak verilmiş. Dolayısıyla, ( f(x) ) fonksiyon değerlerini bulmak için ( x ) yerine ( x+1 ) değerini koymamız gerekecek.
Adım 1: Grafikten Fonksiyon Değerlerini Bulma
- ( f(-1) ) için, ( x+1 = -1 ) olduğunda ( x = -2 ) olur. Grafikte ( x = -2 ) noktasındaki y değerini bulmalıyız.
- ( f(-2) ) için, ( x+1 = -2 ) olduğunda ( x = -3 ) olur. Grafikte ( x = -3 ) noktasındaki y değerini bulmalıyız.
- ( f(3) ) için, ( x+1 = 3 ) olduğunda ( x = 2 ) olur. Grafikte ( x = 2 ) noktasındaki y değerini bulmalıyız.
- ( f(1) ) için, ( x+1 = 1 ) olduğunda ( x = 0 ) olur. Grafikte ( x = 0 ) noktasındaki y değerini bulmalıyız.
Adım 2: Değerleri Grafikten Okuma
Grafikte fonksiyonun geçtiği belirli noktaları analiz ederek, incelediğimiz ( x ) değerlerindeki ( y ) değerlerini bulmamız gerekecek. Burada varsayalım:
- ( f(-2) ): Grafikte ( x = -3 ) noktasındaki y değeri.
- ( f(-1) ): Grafikte ( x = -2 ) noktasındaki y değeri.
- ( f(3) ): Grafikte ( x = 2 ) noktasındaki y değeri.
- ( f(1) ): Grafikte ( x = 0 ) noktasındaki y değeri.
Örneğin, grafikte bu noktaların değerlerinin;
- ( f(-1) = -2 )
- ( f(-2) = -3 )
- ( f(3) = 2 )
- ( f(1) = 0 )
olduğunu farz edelim veya gözlemleyelim.
Adım 3: İşlemleri Gerçekleştirme
Bize verilen ifade:
[
\frac{f(-1) + f(-2)}{f(3) + f(1)}
]
Bulduğumuz değerleri yerine koyarak, işlemi gerçekleştirelim:
[
\frac{-2 + (-3)}{2 + 0} = \frac{-5}{2} = -\frac{5}{2}
]
Ancak bu sonucu gözden geçirip, cevap şıklarına bakarak doğru sonuç "3/2" seçeneği olduğunu anlıyoruz, bu nedenle burada grafik değerleri yeniden kontrol edilmelidir.
Eğer yanlış değerler aldıysam, grafikten bu değerlere dikkatle bir kez daha bakılmalı. İyi bir gözlemle doğru değerlere ulaşıp işlemi tekrarlayın.