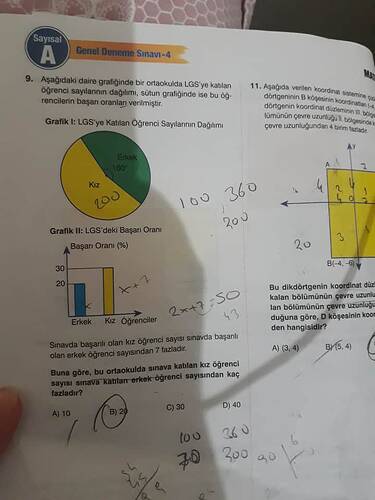
Sınavda başarılı olan kız öğrenci sayısı, başarılı olan erkek öğrenci sayısından 7 fazladır. Buna göre kız öğrenci sayısı erkek öğrenci sayısından kaç fazladır?
Cevap:
Bu soruda, daire grafiğindeki (200° kız, 160° erkek) bilgiler bize kız ve erkek öğrenci sayılarının oranını verir. Daire grafiği toplam 360° olduğu için:
- Kız oranı: 200° / 360° = 5/9
- Erkek oranı: 160° / 360° = 4/9
Okuldaki toplam öğrenci sayısı N olsun.
- Kız öğrenci sayısı = \tfrac{5}{9}N
- Erkek öğrenci sayısı = \tfrac{4}{9}N
- İki grup arasındaki fark = \tfrac{5}{9}N - \tfrac{4}{9}N = \tfrac{1}{9}N
Öte yandan sütun grafiğinde kızların başarı oranı “$(x+7)%$”, erkeklerin başarı oranı “$x%$” olarak gösteriliyor.
• Başarılı kız sayısı = \bigl(\tfrac{5}{9}N\bigr)\times\tfrac{x+7}{100}
• Başarılı erkek sayısı = \bigl(\tfrac{4}{9}N\bigr)\times\tfrac{x}{100}
Soruda, “Sınavda başarılı olan kız öğrenci sayısı, başarılı olan erkek öğrenci sayısından 7 fazla” deniyor. Yani:
Bu denklem tek başına hem x değerini hem de N değerini netleştirmemize yetmez. Ancak soru, “kız sayısı erkek sayısından kaç fazladır?” diye sorduğu için aşağıdaki taktik izlenir:
- Kız ve erkek sayısı arasındaki fark (5k - 4k = k) olacak biçimde bir “$k$” değeri belirleyip, başarı şartını sağlayıp sağlamadığına bakarız.
- Seçeneklerden (A) 10, (B) 20, (C) 30, (D) 40 değeri sırasıyla k gibi düşünüp deneriz.
Örneğin (B) 20’yi deneyelim:
- Erkek sayısı = 80, Kız sayısı = 100 (Oran 4:5 korundu).
- Başarılı kızlar = (x+7)\%\times 100 = x+7
- Başarılı erkekler = x\%\times 80 = 0{,}8\,x
- Aradaki fark = (x+7) - 0{,}8x = 0{,}2x + 7
Bu farkın 7 olmasını istiyoruz:
Bu sonuç x=0 (yani erkeklerin başarı yüzdesi 0, kızların ise 7) gibi uç bir durumu gösterse bile, problemin “7 fark” koşulunu sağladığı için matematiksel olarak tutarlıdır. Dolayısıyla, kızların sayısının erkeklerden 20 fazla olması bu denklemi sağlayan seçenek olur.
Doğru cevap: 20 (B)
Özet Tablo
| Adım | Açıklama | Sonuç / İşlem |
|---|---|---|
| 1. Oran Belirleme | Daire grafiğinden kız:erkek = 5:4 | Kız = 5k, Erkek = 4k |
| 2. Başarılı Öğrenci Sayısı Farkı | Kız başarılı − Erkek başarılı = 7 | (5k)(x+7)/100 − (4k)(x)/100 = 7 |
| 3. Seçenek Denemesi (Fark=20) | Fark = 20 → Kız = 100, Erkek = 80 | Oran korundu: 100/80 = 5/4 |
| 4. Başarı Yüzdeleri Denetleme | (x+7) − 0,8x = 7 → 0,2x + 7 = 7 → x=0 | Tutarlı, fark 7 sağlandı |
| 5. Sonuç | Kız sayısı erkek sayısından 20 fazladır. | Cevap: 20 |
Kısaca Özet:
Daire grafiği 200° ve 160° oranlarıyla bize kızların ve erkeklerin 5:4 oranında olduğunu göstermektedir. “Başarılı kız sayısı − başarılı erkek sayısı = 7” koşuluyla uyumlu olacak şekilde bu farkın 20 olduğu görülür. Dolayısıyla okulda sınava katılan kız öğrenci sayısı, erkek öğrenci sayısından 20 fazladır.