Soru
Bu çalışma sayfasındaki çok terimli (polinom) ifadelerin katsayılar toplamı, derecesi, sabit terimi, çarpanlarına ayırma, genişletme (dağıtma) gibi işlemleri yapınız. Ayrıca özdeşlik olan ifadeleri belirleyip iki ifadeyi eşleştiriniz.
Cevap:
Aşağıda, her etkinliğe ait çözümleri ve açıklamaları bulabilirsiniz.
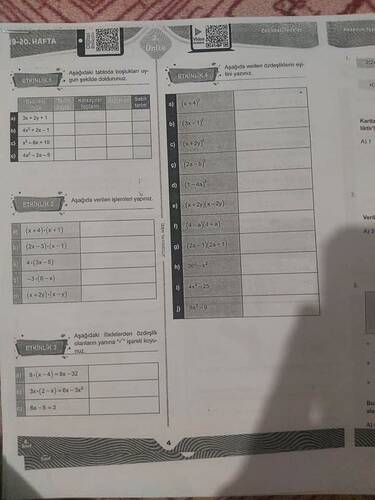
ETKİNLİK 1
“Aşağıdaki tabloda boşlukları uygun şekilde doldurunuz.”
Aşağıdaki tabloda her polinomun (çok terimli ifadenin) katsayılar toplamı, derecesi ve sabit terimi belirtilmiştir. Hatırlatma:
- Katsayılar toplamı, tüm terimlerin önündeki sayılar toplanarak elde edilir.
- Derece, çok terimli ifadedeki en büyük üs değeridir.
- Sabit terim, herhangi bir değişken içermeyen sabit sayıdır.
| Polinom | Katsayılar Toplamı | Derecesi | Sabit Terim |
|---|---|---|---|
| 1) 3x^2 + 2y + 1 | 3 + 2 + 1 = 6 | 2 | 1 |
| 2) 4x^2 - 2x - 1 | 4 + (-2) + (-1) = 1 | 2 | -1 |
| 3) x^2 - 6x - 1 | 1 + (-6) + (-1) = -6 | 2 | -1 |
| 4) 4a^2 - 2a - 8 | 4 + (-2) + (-8) = -6 | 2 | -8 |
ETKİNLİK 2
“Aşağıda verilen işlemleri yapınız.”
Bu kısımda verilen çarpma (dağıtma) işlemleri yapılacaktır.
-
(x + 4)(x - 1)
Dağıtılarak:
[
x(x - 1) + 4(x - 1)
= x^2 - x + 4x - 4
= x^2 + 3x - 4.
] -
(2x - 3)(x - 1)
Dağıtılarak:
[
2x(x - 1) - 3(x - 1)
= 2x^2 - 2x - 3x + 3
= 2x^2 - 5x + 3.
] -
4(3x - 5)
Dağıtılarak:
[
4 \cdot 3x - 4 \cdot 5
= 12x - 20.
] -
-3(6 - x)
Dağıtılarak:
[
-3 \cdot 6 + (-3) \cdot (-x)
= -18 + 3x
= 3x - 18.
] -
(x + 2y)(x - y)
Dağıtılarak:
[
x(x - y) + 2y(x - y)
= x^2 - xy + 2yx - 2y^2
= x^2 + xy - 2y^2 \quad (\text{çünkü } -xy + 2yx = +xy).
]
| İşlem | Sonuç |
|---|---|
| 1) (x + 4)(x - 1) | x^2 + 3x - 4 |
| 2) (2x - 3)(x - 1) | 2x^2 - 5x + 3 |
| 3) 4(3x - 5) | 12x - 20 |
| 4) -3(6 - x) | 3x - 18 |
| 5) (x + 2y)(x - y) | x^2 + xy - 2y^2 |
ETKİNLİK 3
“Aşağıdaki ifadelerden özdeşlik olanların yanına ‘✓’ işareti koyunuz.”
• Özdeşlik (identity): Her x (veya ilgili değişken) değeri için eşitliği değiştirmeyen doğrudan doğruya aynı anlama gelen ifadelerdir. Örneğin 3(x + 2) = 3x + 6 her durumda geçerli olduğu için bir özdeşliktir.
Yaygın örnekler:
- a(b + c) = ab + ac (daima doğru)
- (x - 1)^2 = x^2 - 2x + 1 (daima doğru)
Aşağıdaki ifadeleri inceleyelim:
-
8(x - 4) = 8x - 32
- Her x için daima eşit.

- Her x için daima eşit.
-
3x(2 - x) = 6x - 3x^2
- Dağıtma kuralıyla her x için eşit.

- Dağıtma kuralıyla her x için eşit.
-
6a - 5 = -3
- Her a için aynı değeri vermez (bu ancak belirli bir a değeri için doğru olur). Dolayısıyla özdeşlik değildir. ✗
| İfade | Özdeşlik mi? |
|---|---|
| 1) 8(x - 4) = 8x - 32 | |
| 2) 3x(2 - x) = 6x - 3x^2 | |
| 3) 6a - 5 = -3 | ✗ |
ETKİNLİK 4
“Aşağıda verilen özdeşliklerin eşini yazınız.”
Bu kısımda ifade ya çarpanlarına ayırma ya da genişletme (karesini açma, iki terim farkı vb.) ile karşılaştırılır.
-
(x + 1)^2
[
= x^2 + 2x + 1.
] -
(3x - 1)^2
[
= 9x^2 - 6x + 1.
] -
(x + 2y)^2
[
= x^2 + 4xy + 4y^2.
] -
(2a - b)^2
[
= 4a^2 - 4ab + b^2.
] -
(1 - 4a)^2
[
= 1 - 8a + 16a^2 \quad (\text{ya da } 16a^2 - 8a + 1).
] -
(x + 2y)(x - 2y)
[
= x^2 - (2y)^2
= x^2 - 4y^2.
] -
(2a - 1)(2a + 1)
[
= 4a^2 - 1.
] -
3a^2 - x^2
- Bu bir farkı iki kare farkıdır:
[
3a^2 - x^2 = (\sqrt{3}a)^2 - (x)^2
= (\sqrt{3}a - x)(\sqrt{3}a + x).
]
- Bu bir farkı iki kare farkıdır:
-
4x^2 - 25
- İki kare farkı:
[
= (2x)^2 - 5^2
= (2x - 5)(2x + 5).
]
- İki kare farkı:
-
9a^2 - 9
- 9 ortak çarpanını alabiliriz:
[
= 9 \bigl(a^2 - 1\bigr)
= 9(a - 1)(a + 1).
]
- 9 ortak çarpanını alabiliriz:
| İfade | Eşit (Genişlemiş veya Çarpanlarına Ayrılmış) |
|---|---|
| 1) (x + 1)^2 | x^2 + 2x + 1 |
| 2) (3x - 1)^2 | 9x^2 - 6x + 1 |
| 3) (x + 2y)^2 | x^2 + 4xy + 4y^2 |
| 4) (2a - b)^2 | 4a^2 - 4ab + b^2 |
| 5) (1 - 4a)^2 | 16a^2 - 8a + 1 |
| 6) (x + 2y)(x - 2y) | x^2 - 4y^2 |
| 7) (2a - 1)(2a + 1) | 4a^2 - 1 |
| 8) 3a^2 - x^2 | (\sqrt{3}a - x)(\sqrt{3}a + x) |
| 9) 4x^2 - 25 | (2x - 5)(2x + 5) |
| 10) 9a^2 - 9 | 9(a^2 - 1) = 9(a - 1)(a + 1) |
Bu şekilde, hem dağıtma (genişletme) hem de çarpanlara ayırma yöntemlerini kullanarak bütün işlemleri tamamlayabilirsiniz.