Matematik Alıştırmaları Çözümü
Merhaba! Sorular üzerinden gidelim:
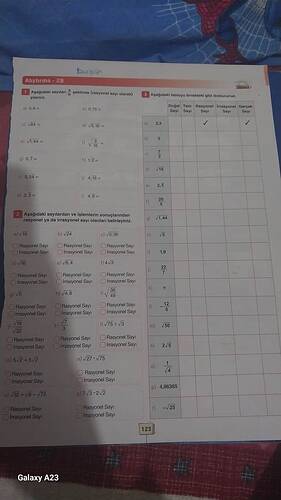
1. Rasyonel Sayı Yazım
Aşağıdaki sayıları \frac{a}{b} şeklinde (rasyonel sayı olarak) yazınız.
-
a) \sqrt{64} = 8 \Rightarrow \frac{8}{1}
-
b) 0.75 = \frac{75}{100} = \frac{3}{4}
-
c) \sqrt{1.44} = 1.2 \Rightarrow \frac{6}{5}
-
d) 0.7 = \frac{7}{10}
-
e) 0.24 = \frac{24}{100} = \frac{6}{25}
-
f) 2.3 = \frac{23}{10}
-
g) \sqrt{0.16} = 0.4 \Rightarrow \frac{2}{5}
-
h) \frac{9}{16} = \frac{9}{16} zaten rasyonel
-
i) 1.2 = \frac{12}{10} = \frac{6}{5}
-
j) 4.18 = \frac{418}{100} = \frac{209}{50}
-
k) 0.49 = \frac{49}{100}
2. Rasyonel ve İrrasyonel Sayılar
Aşağıdaki sayılardan ve işlemlerin sonuçlarından rasyonel ya da irrasyonel sayıları belirleyiniz.
- a) \sqrt{16} - Rasyonel Sayı (Çünkü \sqrt{16} = 4)
- b) \frac{18}{32} - Rasyonel Sayı (Çünkü sadeleşir)
- c) \sqrt{0.36} - Rasyonel Sayı
- d) \sqrt{4/3} - İrrasyonel Sayı
- e) 6/\sqrt{4} - Rasyonel Sayı
- f) \sqrt{3} - İrrasyonel Sayı
- g) 75/\sqrt{3} - İrrasyonel Sayı
- h) \sqrt{8}/3 - İrrasyonel Sayı
- i) 5 \sqrt{2} + 5 \sqrt{2} - İrrasyonel Sayı (Ancak işlemin sonucu rasyonel olabilir)
- j) 7/3 \cdot 2/\sqrt{2} - İrrasyonel Sayı
3. Tablodaki Sayıları Tanımlayın
- a) 2.3 - Gerçek Sayı (Rasyonel)
- b) 1 - Doğal ve Tam Sayı
- c) \frac{7}{2} - Rasyonel Sayı
- d) \sqrt{16} - Doğal, Tam, ve Rasyonel Sayı
- e) 2/5 - Rasyonel Sayı
- f) 20/5 - Doğal, Tam, ve Rasyonel Sayı
- g) \sqrt{1.44} - Rasyonel Sayı
- h) \sqrt{5} - İrrasyonel Sayı
- i) 1.9 - Rasyonel Sayı
- j) \frac{22}{7} - Rasyonel Sayı ama \pi'nin yaklaşık değeridir.
- k) \pi - İrrasyonel Sayı
- l) \frac{12}{6} = 2 - Doğal ve Rasyonel Sayı
- m) \sqrt{50} - İrrasyonel Sayı
- n) \frac{2}{5} - Rasyonel Sayı
- o) \frac{1}{\sqrt{4}} - Rasyonel Sayı
- p) 4.96365 - Rasyonel Sayı
- r) -\sqrt{25} = -5 - Tam ve Rasyonel Sayı
Özet: Rasyonel ve irrasyonel sayıları köklü ya da kesirli ifadeleri çözerek belirleyebilirsiniz. Rasyonel sayılar kesirli veya tam sayılar olarak ifade edilebilirken, irrasyonel sayılar ondalıklı ve tam şekilde yazılamaz.