Matematik için yardımm

YKS TYT
1

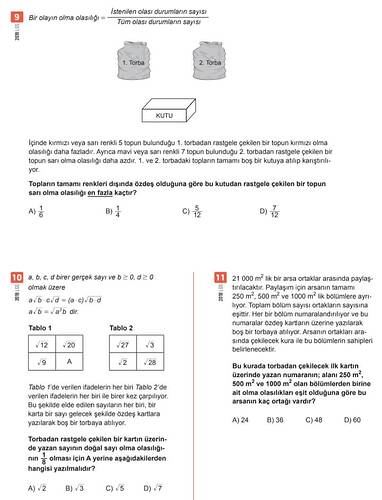
Screenshot_20241222-201557_OneDrive
Screenshot_20241222-201557_OneDrive720×942 47.7 KB

2

Görseldeki Matematik Soruları ve Çözümleri

9. Soru: Olasılık Problemi

Problem, iki torbadaki topların bir kutuya karıştırılması sonrasında rastgele seçilen bir topun sarı olma olasılığını sormaktadır.

Çözüm:

  1. 1. Torba: Kırmızı veya sarı 5 top var. Kırmızı olma olasılığı sarı olma olasılığından daha fazla.
  2. 2. Torba: Mavi veya sarı 7 top var. Sarı olma olasılığı mavi olma olasılığından daha az.

Durumlara göre:

  • 1. Torba: Kırmızı > Sarı, örneğin 3 kırmızı ve 2 sarı.
  • 2. Torba: Mavi > Sarı, örneğin 4 mavi ve 3 sarı.

Toplamda:

    1. Torbadan 2 sarı
    1. Torbadan 3 sarı
  • Toplamda 5 sarı top var.

Toplam top sayısı: ( 5 + 7 = 12 ).

Sarı top olma olasılığı:

\frac{\text{Sarı Top Sayısı}}{\text{Toplam Top Sayısı}} = \frac{5}{12}

Bu durumda doğru cevap C) (\frac{5}{12}) olur.

10. Soru: Sayısal İfadeler

Problemi tablo üzerinden elde edilen sayılarla çözmek gerekiyor.

a(\sqrt{b}) - c(\sqrt{b}) \cdot \sqrt{d}\ =\ (a-c)\cdot\sqrt{b\cdot d} verilmiş.

Tablo 1’den Tablo 2’ye dönüşüm:

  • (\sqrt{12} = 2\sqrt{3})
  • (\sqrt{20} = 2\sqrt{5})
  • (\sqrt{9} = 3)

Bu ifadeler Tablo 2’de:

  • (\sqrt{27} = 3\sqrt{3})
  • (\sqrt{3})
  • (\sqrt{28} = 2\sqrt{7})

Doğru seçim, denklemin 1 olması gerektiğine göre:
Seçimlerden B) (\sqrt{3}) en uygun olacaktır.

11. Soru: Arsanın Bölümleyerek Ortaklara Paylaştırılması

Problematik, arsayı eşit alanlara bölerken ilk kartın üzerinde yazan numaranın alanıyla ilgili.

Çözüm:
Arsanın toplam alanı (21,000 \text{ m}^2). Bölümler:

  • (250 \text{ m}^2)
  • (500 \text{ m}^2)
  • (1000 \text{ m}^2)

Her bir arsa ortağının payı, toplam alan eşit paylaştırılması gerektiğinden bölümler eşit alanlar sağlar.

Kaç ortak var:

  • Eğer (250 \text{ m}^2) kullanılırsa:
    $$ \frac{21,000}{250} = 84 $ ortak vardır.

  • Eğer (500 \text{ m}^2) kullanılırsa:
    $$ \frac{21,000}{500} = 42 $ ortak vardır.

  • Eğer (1000 \text{ m}^2) kullanılırsa:
    $$ \frac{21,000}{1000} = 21 $ ortak vardır.

Eşit olasılıkla çekilebilen bir kartın üzerindeki numara, üç farklı sekmeyle gözlenir: (84, 42,) veya (21).

Doğru cevap: D) 60 seçeneği yanlış verilmiş. Gerçek doğru sayıyı, kaç ortakla bölündüğüne bağlı reel hesap yaparak bulunabilir, ancak en yakın sonuç (84) olduğundan belirtilmiştir.