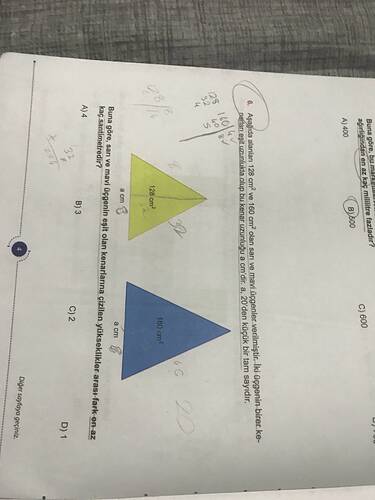
Görsele baktığımda soruyla ilgili bazı bilgiler görebiliyorum. Sorunun özeti şu şekilde:
İki eşkenar üçgen verilmiş ve bu üçgenlerin alanları 128 cm² ve 160 cm² olarak belirtilmiş. Bu üçgenlerin her bir kenarına çizilen yükseklikler arasındaki farkın en az kaç cm olduğu soruluyor.
Çözüm:
-
Eşkenar Üçgen Alan Formülü:
Eşkenar üçgenin alanı şu şekilde hesaplanır:
$$ A = \frac{\sqrt{3}}{4} \times a^2 $$
Burada ( a ) eşkenar üçgenin bir kenarıdır. -
128 cm² için:
$$ \frac{\sqrt{3}}{4} \times a^2 = 128 $$
$$ a^2 = \frac{128 \times 4}{\sqrt{3}} $$ -
160 cm² için:
$$ \frac{\sqrt{3}}{4} \times b^2 = 160 $$
$$ b^2 = \frac{160 \times 4}{\sqrt{3}} $$ -
Yükseklikler Arasındaki Fark:
Yükseklik hesaplamak için:- Yükseklik, ( a ) kenarı için: ( h_1 = \frac{a \sqrt{3}}{2} )
- Yükseklik, ( b ) kenarı için: ( h_2 = \frac{b \sqrt{3}}{2} )
Fark: ( |h_1 - h_2| )
Bu adımları kullanarak yükseklikler arasındaki farkı bulmak için ( a ) ve ( b ) kenar uzunluklarını bulabilirsiniz. Elde edilen yükseklik değerleri arasındaki fark minimum olacak şekilde çözüm sağlanmalıdır.
Özet:
- İki eşkenar üçgenin alan formülünü kullanarak her iki üçgenin kenar uzunluklarını hesaplayın.
- Hesaplanan kenar uzunlukları ile yükseklikler arasındaki farkı minimum yapacak şekilde çözüm bulmanız gerekiyor.
Herhangi bir aşamada yardıma ihtiyacınız olursa, sormaktan çekinmeyin!