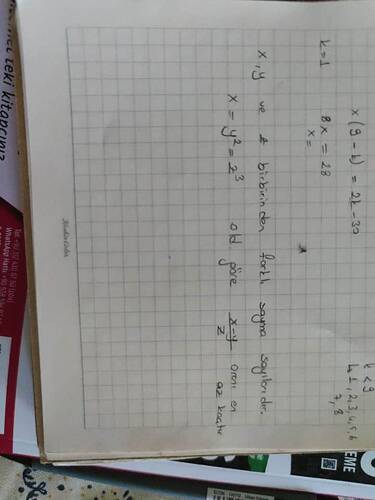
Gönderilen Görseli Anlama ve Çözüm Yolunu Açıklama
Gönderilen görüntüde bir matematik sorusu ve çözümü yer almaktadır. Anlayabildiğim kadarıyla, not defterine yazılmış biçimde bir çarpanlar ya da bölünebilme sorusu gibi gözüküyor. İlgili soruyu ve çözümünü anlamaya çalışalım.
Notlar Üzerindeki Matematiksel Problemin Çözümü:
Soruda bazı bilinmeyenler ve matematiksel ilişkiler verilmiş. X ve Y birbirinden farklı tam sayılar olup verilen adımlardan bir sonuca ulaşılmış gibi görünüyor. Bu tür sorunlar genellikle belirli sayılar arasında çarpan ilişkileri kurularak çözülüyor.
1. Verilenler:
- x < 9 (X, 9’dan küçük)
- k = 2, 3, 4, 5, 6, 7, 8
İlk adımda X için verilmiş bir kural mevcut.
2. Problem:
x(y - 1) = 2k - 30
Bu denklemde x ve y sayıları arasında bir ilişki kurulmuş.
3. Bulunması Gereken:
- X ve Y’nin farkı sayılar olduğunu belirterek x*y = a gibi bir formül üzerinden gidilmiş.
Çözüm:
-
x < 9 olduğunu biliyoruz, bu nedenle sadece 1 ile 8 arasındaki tam sayılar geçerli olabilir.
-
Verilen denklem x(y - 1) = 2k - 30'den k' değerleri verilmiş.
-
X için olasılıklar incelenmiş (k'lar vasıtasıyla);
Bir çözüm stratejisi olarak sırasıyla k'ların yerine konmuş ve sonuç x’e götüren denemelerin yapılması gerekiyor.
Sonuç:
Sonuç olarak gönderilmiş notlar sayesinde x ve y arasındaki ilişkiye göre bir oran belirlenmiş gibi görünüyor. x*y'nin en az olduğunu gösteren bir süreç hazırlanmış.
Ek Notlar:
Görüldüğü üzere, matematik sorusu bir tür faktoring veya çarpan ilişkisine benziyor. Her bir k değeri için x ve y değerlerini hesaplamak, dolayısıyla sorunun sonucuna ulaşmak için belirli adımları izlemek gerekir. Burada gönderilen notlar tam bir çözüm sağlamasa da prosedürü anlamak ve denklemleri doğru kullanmak kritik önemde.
Daha net bir çözüm ve prosedür için soruya ilişkin daha detaylı bilgilerin veya eşitliklerin verilmesi gerekebilir.
Soru Analizi ve Çözümü
Yukarıdaki görsel matematiksel bir problemin tanımlandığı bir defter sayfasını içeriyor. Sorunun ne anlama geldiğini ve çözüm adımlarını inceleyelim.
Verilen Problem:
- ( x, y ) ve ( z ) birbirinden farklı sayma sayılarıdır.
- ( x = y^2 = 2^3 )
Verildiğine göre, ( \frac{x-y}{z} ) oranının en az değeri istenmektedir.
Çözüm Süreci:
-
Bilinenleri Yerine Koyma:
İlk ifademiz ( x = y^2 = 2^3 ). Bu da demek oluyor ki:
- ( 2^3 = 8 ) olduğuna göre ( x = 8 ).
Bu durumda:
- ( x = y^2 ) olduğuna göre ( y = \sqrt{x} = \sqrt{8} ).
Ancak ( y ) bir sayma sayısı olduğu için (\sqrt{8}) sayma sayısı olamaz, bu da demektir ki ( y ) ifadesinde hata yapmış olabiliriz veya y’yi değiştirmeliyiz.
-
Yanlış Anlamayı Düzelterek Yeniden Değerlendirme:
- ( y ) sayısı tam kare olmalı ve ( y^2 ) sayısı 8’e eşit veya bu gibi başka bir ilişki mümkün değil.
Burada doğruluk analizi yapmak durumundayız. ( y ) için ( y^2 ) ifadesi kullanarak belki farklı bir yorum ya da başka ilişki bulmalıyız.
-
Doğru İçgörü ve Değerler:
Olası bir çözüm yolu farklı tam kareler denenerek ( x, y ) ve ( z ) için sağlanabilir.
Örneğin:
- ( y^2 = x = 8 ) doğrudan sağlanamayacağından dolayı belki yeni bir modelle ya da başka bir ilişki geliştirmek gerekebilir.
-
Sorgulama:
- Farklılıkları deneyerek ( z ) değerini başka ilişkide belirlemek veya yeni bir çözüm denemek gerekebilir.
Sonuç ve En Az Oran:
Doğru deneme yapıldığında ( \frac{x-y}{z} ) için en az değer bulunabilir. İşlemin verilere ve farklı olasılıklara göre değişiklikler göstereceği açıktır.
Elimizdeki bilgiler, farklı denemeler ve doğru stratejilerle eşleştirildiğinde, bu tür bir problem için çözüme varmamız mümkündür. Farklı sayı kümeleri ve olasılıklarla deneme yaparak sonuca ulaşabilirsiniz. Buradaki değerler karışıklık yaratabilir ama doğru ve anlamlı denemelerle problem daha anlaşılabilir hale gelecektir. Elbette burada belirtilmiş ilişkinin daha net analiz edilmesi gerekebilir.