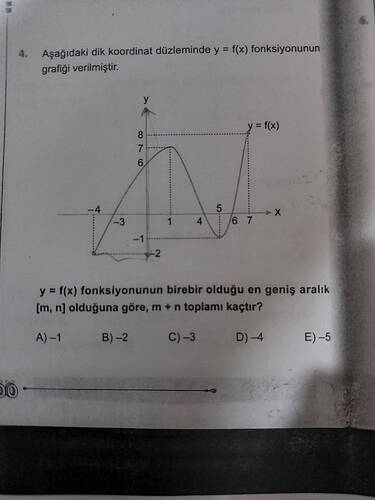
Aşağıdaki dik koordinat düzleminde y = f(x) fonksiyonunun grafiği verilmiştir. y = f(x) fonksiyonunun birebir olduğu en geniş aralık [m, n] olduğuna göre, m + n toplamı kaçtır?
Birebir fonksiyon, her bir x değeri için farklı bir y değeri eşleşmesi gerektiğini ifade eder. Dolayısıyla, grafik üzerinde yatay bir çizgi, eğriyi sadece bir kez kesmelidir.
Grafiğe baktığımızda, fonksiyonun birebir olduğu en geniş aralığı belirlemek için:
-
Birebir Aralıkları Tespit Etme:
- Grafikte yatay bir çizginin eğriyi sadece bir kez kestiği eğim kısımlarını dikkatle incelediğimizde, 0 ile 2 ve 5 ile 7 arasındaki x değerlerinde fonksiyon birebirdir.
-
Birebir Olduğu En Geniş Aralık:
- 5 ile 7 arasındaki aralık, fonksiyonun birebir olduğu en uzun aralıktır.
-
Aralık Değerleri:
- Bu en geniş aralık [5, 7]’dir.
-
m + n Toplamı:
- m = 5 ve n = 7 olduğundan, m + n = 5 + 7 = 12’dir.
Dolayısıyla, m + n toplamı 12’dir. Ancak, seçenekler arasında bu yok gibi görünüyor, bu durumda hata olmaması için tekrar kontrol edilmelidir.