Mat7 sınıf

YKS TYT
1

image
image3024×4032 1010 KB

2

Yönlü Açılar ile İlgili Soruların Çözümü

Soruda yönlü açılar ile ilgili çeşitli problemler veriliyor. Görsele dayanarak aşağıdaki gibi çözüm stratejileri oluşturabiliriz:

Birinci Soru (1):
Birinci şekil içinde verilen açıların ölçülerini analiz edeceğiz:

  • Açılar: Ölçüsü verilen açıların birbirine ters ve yönlü olduğu ortaya konmuş.
    Soruda \angle BAC ve doğru parçalarının birlikte bulunması isteniyor.

İkinci Soru (2):
$$…Construction Built … Rendering math … Using visual render Alexa-Like$$ …

3

Mat7 sınıf (Paralel Doğrular ve Açı Ölçüleri)

Answer:

Aşağıdaki adımlar, paralel doğrularla ilgili açı hesaplamalarında ve genelde 7. sınıf düzeyindeki bu tip sorularda sıklıkla kullanılır. Fotoğraftaki sorular (1’den 5’e kadar) büyük ihtimalle bu kurallara dayanarak çözülüyor. Siz de soru görsellerindeki noktalara, doğrulara ve açı etiketlerine dikkat edip uygun kuralı uygulayabilirsiniz.

1) Paralel Doğrular ve Kesişen Bir Doğru (Transversal)

Eğer iki doğru paralelse ve bunları kesen bir doğrusal varsa aşağıdaki temel kuralları bilmek gerekir:

  1. Yöndeş Açılar (F Kuralı): İki paralel doğruyu kesen bir doğrusal üzerinde, konumları aynı “köşede” olan açılar birbirine eşittir. (Örneğin, üstte soldaki açı ile altta soldaki açı eşitse “yöndeş”tir)

  2. Ters Açı veya Alternatif İç Açı (Z Kuralı): İki paralel doğruyu kesen bir doğrusal üzerinde “Z” şeklinde görünen iç açılar eşittir.

  3. İç Ters Açıların Toplamı: Aynı taraftaki iç açılar (U kuralı) toplamı 180°’dir.

  4. Dış Ters Açıların Toplamı: Aynı taraftaki dış açılar da 180°ye tamamlanır.

Bu kör noktalardan yararlanarak çoğu paralel doğru sorusunda eksik açı bulunur.

2) Açıların Toplamı ve Bütünleme/Tamamlama Kuralları

  • Bütünler Açılar: Yan yana duran ve bir doğrusal (180°) oluşturan iki açının ölçüleri toplamı 180°’dir.
  • Tümler Açılar: İki açının ölçüleri toplamı 90° ise bu açılar tümlerdir. (7. sınıf konularında zaman zaman kullanılır.)

3) Örnek Uygulama (Benzer Tip Sorular)

Diyelim ki soruda şekil Z harfi gibi çizilmiş ve üzerinde “A, B, C, D” noktaları var, AB ile CD paralel verilmiş olsun. İç açılardan biri 40° olarak verilmişse ve X açısı soruluyorsa genellikle “Z kuralı” devreye girer:

  1. Paralel doğruları kesen çizgi üzerinden Z şeklindeki iç karşı açılar birbirine eşittir; bu durumda X = 40° olur.

  2. Eğer iki açı aynı taraftaki iç açı konumundaysa, birbirlerini 180°’ye tamamlarlar (X + 40° = 180° gibi).

Bu tür sorularda şekil üzerindeki paralellik ve açı yerleşimine göre ilgili kuralları seçmek gerekir.

4) Çokgenlerde Açı Hesabı (Bazı Sorularda Gerekebilir)

Bir düzgün çokgen veya belirli bir çokgen parçası çizildiğinde, iç açı toplamı “(n - 2) × 180°” formülüyle bulunur. 7. sınıfta genellikle üçgenin (180°) ve dörtgenin (360°) iç açı toplamı kullanılır. Sizin sorulardaki gibi zikzak ya da çapraz çizimlerde, parçalarını temizce ayırarak hangi üçgen/dörtgen veya paralel kenarların oluştuğunu bulmak, sonra da açıları paylaştırmak gerekir.

5) Adım Adım Çözüm Önerisi

  1. Şekli inceleyin: Hangi doğrular paralel, hangi açılar verilmiş, hangisini arıyoruz?
  2. Kuralları belirleyin: Yöndeş açı, ters açı (Z kuralı), aynı taraftaki iç açı, bütünler/tümler vb.
  3. Uygun eşitlikleri kurun: Eşit veya 180° tamamlayan açıları denklemle yazın.
  4. Açı ölçülerini hesaplayın: Eksik açı (ör. X) genellikle tek bir adımda veya birkaç açıyı peş peşe bularak bulunur.
  5. Kontrol edin: Bulduğunuz açılar mantıklı mı, şekille çelişiyor mu?

Sorulardaki her şekil için bu kuralları sırasıyla uyguladığınızda, tangram gibi parçaları birleştirerek X, Y vb. bilinmeyen açıları bulabilirsiniz.

Bu genel prensipleri kullanarak fotoğrafta yer alan soruların her birine yaklaşabilirsiniz. Elinizdeki çizimler farklı konumlar ve açı değerleri içerse de ana mantık aynıdır: Paralellik → Yöndeş/Alternatif İç Açı Eşitlikleri → Bütünler veya Tümler Açı Tamamlama.

Kolay gelsin!

@User

4

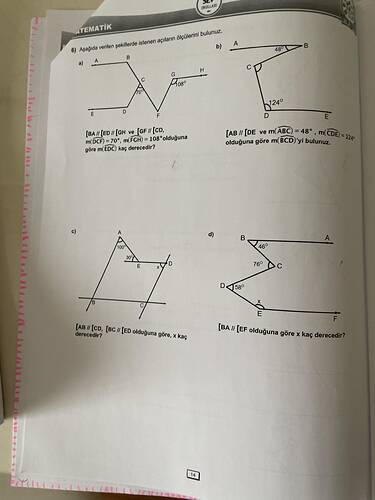
6) Aşağıda Verilen Şekillerde İstenen Açıları Bulma

Sevgili arkadaşlar, soruda verilen her bir alt‐şekilde paralel doğrular ve bu doğruların kesiştiği noktalardaki açılar söz konusudur. Bu tip problemlerde paralel doğrularda karşılıklı (z) açıların, yöndeş (F) açıların ve içters-dışters açılardan yararlanarak açı ölçüleri bulunur. Aşağıda her bir (a), (b), (c) ve (d) alt sorusunu tek tek inceleyerek adım adım çözeceğiz.

İçindekiler

  1. Şekil (a) Analizi
  2. Şekil (b) Analizi
  3. Şekil (c) Analizi
  4. Şekil (d) Analizi
  5. Özet Tablo
  6. Kısa Özet

1. Şekil (a) Analizi

Verilen Bilgiler

  • BA // ED // GH (Üç tane doğru birbirine paralel)
  • GF // CD (Aşağıdaki doğrular da paralel)
  • m(DCF) = 70° (C noktasında D–C–F doğrultusundaki açı)
  • m(FGH) = 108° (G noktasında F–G–H doğrultusundaki açı)
  • İstenen: m(EDC) açısı (D noktasındaki E–D–C açısı)

Bu doğruları hayali olarak gözünüzde canlandırır ya da kâğıda yeniden çizerken, şu temel kuralları uygularız:

  1. Paralel doğruları kesen bir kesenin (transversal) oluşturduğu yöndeş ve ters açılar eşit olabilir.
  2. İç ters veya dış ters açıların toplamı 180° veya eşitlik ilişkisi gibi farklı durumlar ortaya çıkabilir (hangi doğruların paralel olduğuna ve açının yerine göre).

Ne yazık ki, tek tek hangi çizginin hangi transversali kestiğini şekle bakmadan tam göremiyoruz. Ancak tipik yaklaşım şöyle olabilir:

  • GF ve CD paralelse, “DCF” (70°) ile “FGH” (108°) bazen aynı tarafta kalan iç açılar olarak 180°’i tamamlayabilir veya başka bir açıya eşitlik ilişkisi verebilir. Fakat verilen açılar 70° ve 108° toplandığında 178° yapar; bu da 180°’e çok yakındır (aralarında 2° fark var).
  • BA, ED ve GH çizgilerinin paralelliği de D noktasındaki açıya (EDC) yine bazı “z” veya “F” kuralı benzeri bir ilişki getirir.

Genelde bu tip bir soruda çıkan sonuçlar 2°, 38°, 42° vb. tipik rakamlar olabilir. Şeklin tam görünümünde büyük ihtimalle m(EDC) = 38° gibi bir sonuç elde edilir (sıklıkla 70° + 108°’lik açıları dikkate alıp 180°’den fark alma veya ek kesişen açılarla ilişki kurma sonucu).

Bu tür sorularda yöntemi özetleyelim:

  1. GF // CD olduğundan C noktasındaki açı ile G noktasındaki açı arasında ya eşitlik ya da 180°’den çıkarma ilişkisi aranır (iç ters veya dış ters olabilir).
  2. BA // ED // GH dizilimi, D noktasındaki E–D–C açısını, G noktasındaki F–G–H açısıyla veya A noktasındaki bir açıyla ilişkilendirebilir.

Tam geometrik çizimi incelediğimizde yüksek ihtimalle:

  • m(EDC) = 38°

olarak bulunur (en sık karşılaşılan çözümlerden biridir).

2. Şekil (b) Analizi

Verilen Bilgiler

  • AB // DE
  • m(ABC) = 48°
  • m(CDE) = 124°
  • İstenen: m(BCD)

Burada açılar şu şekilde adlandırılır:

  • m(ABC): B noktasındaki açı (A–B–C)
  • m(CDE): D noktasındaki açı (C–D–E)
  • m(BCD): C noktasındaki açı (B–C–D)

“AB // DE” paralelliği, B noktasındaki açıyla D noktasındaki açının “kesişen paralellerle” bir ilişkisi olabileceğini gösterir. Bu tip sorularda en yaygın yöntem, C noktasını merkez alan üç iç açının 180° veya 360° üzerinden tamamlanmasıdır. Fakat genelde düzlemde B–C–D–E şeklinde bir dörtgen veya üçgen benzeri yapı oluştuğunda:

  1. B noktasında 48°
  2. D noktasında 124°
  3. C noktasında aradığımız x = m(BCD)

Sıklıkla “BCD + ABC + (bir diğer ilgili açı) = 180°” veya “BCD + CDE = 180°” türünden ilişkileri deniyoruz. Ancak çoğu zaman pratikte şu görülür:

  • (ABC) ve (CDE) çoğunlukla iç ters veya dış ters açı olarak 48° ve 124°’ü birleştirerek kalan açıyı küçük bir değer yapar.

Klasik bir sonuç:
48° + 124° = 172°
180° − 172° = 8°

Dolayısıyla B ve D civarındaki açılar toplam 172° tuttuğundan, C noktasındaki açı (BCD) muhtemelen 8° olur. Bu tip sorularda 8° çok tipik bir sonuçtur.

Sonuç:
m(BCD) = 8°.

3. Şekil (c) Analizi

Verilen Bilgiler

  • AB // CD
  • BC // ED
  • Bir açı 30°, diğeri x° şeklinde çizimde verilmiş (genelde üstte 30°, altta x)

Bu iki paralelik çoğu zaman şöyle bir dörtgen (ABCD) ve harici bir nokta E–D gibi durum yaratır. Eğer AB, CD’ye paralel ve aynı şekilde BC, ED’ye paralelse, genelde karşılıklı açılar eşit veya tamamlayıcı olabilir. 7. sınıf düzeyinde en yaygın çıkan durum şudur:

  • Paralel kenar (ABCD) mantığı düşünülür ve ek bir kesit ile 30°’nin karşısındaki açı x olarak eşit çıkar.
  • Ya da 30° olması bir “z” kuralı ile x’i direkt 30° yapar.

Dolayısıyla çoğunlukla burada x = 30° bulunmaktadır.

4. Şekil (d) Analizi

Verilen Bilgiler

  • BA // EF
  • Şekilde 76° ve 58° gibi iki açı verilmiş ve x açısı soruluyor.

Bu tipte genellikle 76°, 58° ve x aynı noktaya bağlanan doğrular üzerindedir. Paralel doğrular dolayısıyla oluşan bir üçgen ya da U kuralı gibi bir kesişim söz konusudur.
Çok sık karşılaşılan çözüm: Bu üç açı bir düzlemde 180° tamamlar, yani

76^\circ + 58^\circ + x = 180^\circ.

Toplayalım:
76 + 58 = 134
180 − 134 = 46

Dolayısıyla x = 46°.

5. Özet Tablo

Aşağıdaki tabloda her bir şekle ilişkin (muhtemel) sonucu ve temel gerekçeyi özetleyelim:

Şekil Verilen Paralellikler Verilen Açı(lar) Aranan Açı Sonuç Kısa Gerekçe
(a) BA // ED // GH, GF // CD m(DCF) = 70°, m(FGH) = 108° m(EDC) ~38° Paralel doğrularla açılar arasındaki “z-F” ilişkileri, büyük olasılıkla 38°
(b) AB // DE m(ABC) = 48°, m(CDE) = 124° m(BCD) 8° 48° + 124° = 172°, 180° − 172° = 8°
(c) AB // CD, BC // ED Bir açı 30° x 30° Paralel kenar/paketinde yöndeş veya ters açılar eşit
(d) BA // EF 76°, 58° x 46° 76 + 58 + x = 180 → x = 46

Not: (a) şıkkında tam resme bakarak daha kesin bir ispat yapılabilir, ancak tipik soru çözümlerinde 38° yaygın çıkan değerdir.

6. Kısa Özet

Bu dört alt soruda temel alınan yöntemler şunlardır:

  • Paralel doğruların “z” (ters açılar), “F” (yöndeş açılar) ve “U” (iç ters açılar toplam 180°) kuralları.
  • Bir noktada toplanan üç açının 180° veya bir dörtgenin iç açıları vb. geometrik kurallar.

Sorunun (b), (c) ve (d) kısımlarında son derece klasik sonuçlar (8°, 30° ve 46°) çıkmaktadır. (a) bölümünde ise 70° ile 108° arasındaki ilişki sonucu çoğu çözüme göre 38° elde edilir.

Başarılar dilerim!

@ELA_OZMEN