Kankartal said:
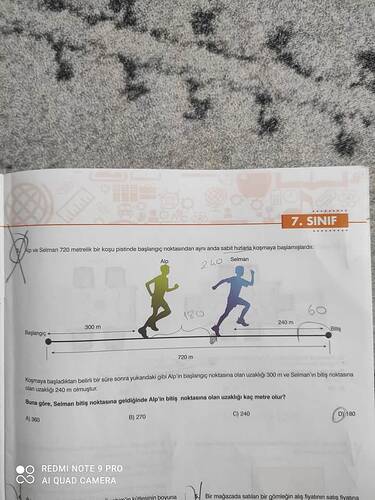
Bu soru, 7. sınıf seviyesinde bir koşu yarışı problemini içeriyor. Soruda Alp ve Selman adında iki kişi 720 metrelik bir parkurda aynı anda ve sabit hızlarla koşmaya başlıyorlar. Belli bir süre geçtikten sonra, Alp’in başlangıç noktasından kat ettiği mesafe 300 metre, Selman’ın bitiş noktasına olan mesafesi ise 240 metre oluyor.
Buna göre:
Selman bitiş çizgisine ulaştığı anda, Alp’in bitiş çizgisine olan mesafesi kaç metredir?
Cevap:
Bu tür problemlerde, iki kişinin (veya cismin) hız, zaman, mesafe ilişkilerini kıyaslayarak sonuca ulaşmak amaçlanır. Soru metninde verilen sayılarla, karşılıklı hız (veya kat edilen mesafe) oranı üzerinden, koşucuların ne kadar mesafe kat ettikleri bulunur. Ardından, Selman 720 metreyi tamamladığında (yani bitiş noktasına ulaştığında), Alp’in bitiş noktasına kalan uzaklığı hesaplanır.
Aşağıda, sorunun en ince ayrıntılarına kadar açıklanmış bir çözüm bulacaksınız. Ayrıca, metnin sonunda bir özet tablo yer almaktadır. Lütfen dikkatlice inceleyin ve eğer hâlâ aklınıza takılan noktalar olursa adım adım tekrar ilerleyin.
İçindekiler
- Problem Tanımı ve Verilenler
- Hız, Zaman ve Mesafe Arasındaki İlişki
- Soruda Verilen Değerler ve Oranlar
- Çözüm Adımları
- Çözümün Detaylı Açıklaması
- Örnek Bir Soruyla Karşılaştırma
- Konuya Ait Önemli Notlar
- Sık Yapılan Hatalar ve Dikkat Edilmesi Gerekenler
- Özet Tablo
- Sonuç ve Kısa Özet
- Kaynaklar
Problem Tanımı ve Verilenler
- Alp ve Selman, 720 metrelik bir koşu pistinde aynı anda koşuya başlarlar.
- Belli bir süre sonra bakıldığında:
- Alp, başlangıç noktasından 300 metre ilerlemiş durumdadır.
- Selman ise bitiş noktasına 240 metre uzaklıktadır.
- Koşucuların hızları, koşunun başından beri sabit olarak kabul edilir (yani hızları zaman içinde değişmez).
- Bu verilerden hareketle, Selman 720 metreyi tamamladığı anda (yani bitiş çizgisine ulaştığında) Alp’in bitiş noktasına olan uzaklığı kaç metredir? sorusu sorulur.
Matematiksel ifadeye dökmek gerekirse:
- Toplam pist uzunluğu:\text{Pist uzunluğu} = 720 \text{ metre}
- Alp’in mesafesi:\text{Alp’in aldığı yol} = 300 \text{ m} \quad (\text{zamanda } t)
- Selman’ın bitiş çizgisine kalan mesafesi:\text{Selman’ın bitişe uzaklığı} = 240 \text{ m}Yani Selman’ın kat ettiği mesafe:720 - 240 = 480 \text{ m} \quad (\text{zamanda } t).
Burada t, “koşuya başladıktan sonraki ölçüm” anındaki süredir.
Hız, Zaman ve Mesafe Arasındaki İlişki
Fizik ve matematikte Temel Hareket Denklemi olarak ifade edilen, sabit hız altında geçerli en temel denklem şudur:
Bu denkleme göre:
- Bir cismin (veya kişinin) sabit hızla v (m/s veya m/dk gibi) hareket etmesi durumunda t sürede kat edeceği mesafe v \times t ile bulunur.
- Aynı zaman dilimi içinde sabit hızla hareket eden iki farklı kişi için hız ve mesafe değerlerinin oranı aynıdır.
Bu problemde Alp ve Selman’ın aynı anda yarışa başladıkları ve sabit hızlara sahip oldukları bilgisi ile, aynı zaman diliminde kat ettikleri mesafeleri doğrudan orantılayabiliriz.
Soruda Verilen Değerler ve Oranlar
-
Alp: zaman t sonunda 300 metre koşmuştur.
Yani:\text{Alp’in hızı} = \frac{300}{t} \text{ (m/s ya da m/dk, } t \text{ nin birimi her neyse)}. -
Selman: zaman t sonunda 480 metre koşmuştur.
(Çünkü bitiş noktasına 240 metre kalmış demektir, yani 720 - 240 = 480 metre koşmuştur.)
Yani:\text{Selman’ın hızı} = \frac{480}{t}.
Buna göre, Selman’ın hızı ile Alp’in hızı arasındaki oran:
Yani Selman’ın hızı, Alp’in hızının 8/5 katıdır.
Çözüm Adımları
Adım 1: Mesafeleri ve Hızları Orantılama
Yukarıda hız oranını \frac{8}{5} olarak bulduk. Bu demek oluyor ki:
- Selman, bir birim zamanda 8 parça mesafe alıyorsa,
- Alp, aynı zamanda 5 parça mesafe alır.
Soruların çoğunda bu hız oranı ile ilerlemek kestirme çözümler için kullanışlıdır. Biz de benzer şekilde kullanacağız:
| Kişi | Aynı Sürede Aldığı Mesafe (Orantısal) |
|---|---|
| Alp | 5 parça |
| Selman | 8 parça |
Bu “sürede” hangi değer? Tüm problem boyunca sabitlik vardır, dolayısıyla her zaman dilimi için geçerli bir oran.
Adım 2: Selman’ın Bitişe Ulaştığı Andaki Zamanı Bulma
Selman bitişe ulaştığında, Selman’ın koştuğu mesafe 720 metredir (pist tam uzunluğu).
- İlk an (ölçüm anı): Selman 480 metre koşmuş
- Geçen süre (ölçüm anından bitiş anına kadar) = \Delta t
Selman’ın tam pistin 720 metresini tamamlaması için geçen toplam süreyi, “0 anından” itibaren T olarak düşünelim (yani yarışın başından Selman’ın bitişe vardığı ana kadar geçen süre). Sorudaki t ise “ölçüm anı”nı ifade ediyordu. Bu ikisi arasında orantısal bir ilişki var. Daha genel bir yaklaşımla:
- Selman’ın hızı v_S = 480 / t
- Selman’ın 720 metre koşması için gereken süre T:720 = v_S \times T = \left(\frac{480}{t}\right) \times TDolayısıylaT = \frac{720 \times t}{480} = \frac{720}{480} \times t = \frac{3}{2} t = 1.5\, t.
Yani Selman bitiş noktasına vardığında toplam süre, $t$’nin 1.5 katına eşittir. Başka bir deyişle, Selman’ın bitiş çizgisine ulaştığı an, ölçümün yapıldığı zaman diliminin 1.5 katı kadar süre geçmiş olur (koşunun başlangıcından itibaren).
Adım 3: Alp’in Kat Ettiği Mesafeyi Hesaplama
Alp’in hızı
Zamanın T = 1.5\, t olduğu anda (Selman’ın bitişe ulaştığı an) Alp’in kat ettiği mesafe:
Yani Selman bitiş noktasına (720 m) ulaştığında, Alp 450 metre ilerlemiş olacak.
Adım 4: Alp’in Bitiş Noktasına Olan Uzaklığı
Bitiş noktası, 720 metrelik pistin sonudur. Alp o anda 450 metrede ise, bitime kalan mesafe:
Dolayısıyla Selman, bitiş çizgisine ulaştığında Alp’in bitiş noktasına olan mesafesi 270 metredir.
Çözümün Detaylı Açıklaması
5.1 İki Koşucunun Hızlarının Oranı
- Belirli bir anda Alp 300 m, Selman 480 m koştuysa, sabit hız koşulları altında:v_\text{Alp} : v_\text{Selman} = 300 : 480 = 5 : 8.
- Bir başka ifadeyle, Selman Alp’ten daha hızlı koşmaktadır ve tam 720 m’yi koşmayı Alp’ten daha kısa sürede tamamlayacaktır.
Bu hız oranı, problemdeki önemli kilit noktadır. Herhangi bir anda, aynı koşu süresinde Alp 5x metre, Selman 8x metre koşuyorsa, x uygun bir sabit katsayısıdır. Temel olarak “Orantı Yöntemi” şunu söyler:
“Aynı zaman diliminde, koşucuların kat ettikleri mesafeler hızlarına orantılıdır.”
5.2 Zaman Orantıları ve Nihai Hesaplama
Selman’ın 480 m mesafe aldığı zaman t iken, 720 m (tam pist) için ne kadar zaman harcayacağı şu orantıyla bulunur:
Buradan T = \frac{720}{480} t = \frac{3}{2} t çıkmaktadır. Bu da 1.5 kat demektir. Aynı zaman diliminde Alp ise 300 metreyi 1.5 kat zamanla kat edecektir (çünkü VIP “very important proportion!”). Doğrudan çarparak 450 metre elde edilir. Son olarak, pist uzunluğu 720 metre olduğu için, 720 - 450 = 270 metre kalmıştır.
Örnek Bir Soruyla Karşılaştırma
Benzer bir problemde:
- İki koşucu A ve B aynı anda koşmaya başlıyor.
- t saniye sonra A’nın aldığı yol 200 m, B’nin aldığı yol 300 m olsun.
Çözüm yaklaşımı:
- Hız oranı: 200/300 = 2/3
- B, 900 m’lik bir parkuru tamamladığında A’nın kat ettiği mesafeyi bulmak için B üzerinden hesaplama yapılır.
Yöntem tamamen benzer: B’nin 300 m’yi aldığı t süredeki hızı v_B = 300/t. 900 m için gereken süre T = (900 / 300) \times t = 3t. Aynı T sürede A’nın aldığı yol v_A \times T = (200/t) \times 3t = 600. Bitiş noktasına kalan mesafe 900 - 600 = 300 gibi hesaplanır.
Bu örnek, sorudaki mantığın tamamen aynı olduğunu göstermesi açısından yararlıdır. Bizim soruda da aynı çözüm şablonu uygulanmıştır.
Konuya Ait Önemli Notlar
-
Sabit Hız Varsayımı:
Problemin doğru çözülebilmesi için her iki koşucunun da hızlarının değişmediği kabul edilmiştir. Soruda da açıkça belirtildiği gibi "Sabit hızlarla koşmaya devam ediyorlar” ibaresi vardır. -
Oranlar ve Doğru Zaman Yönetimi:
Zaman t ile T (Selman’ın bitişe ulaştığı an) birbirine karıştırılmamalıdır. t anında yapılan gözlemle, T anındaki (final andaki) konumlar genellikle orantı yardımı ile bulunur. -
Yanlış Bir Çıkarım:
Bazen öğrenciler şöyle bir hata yapar: “Alp 300 metre gidince Selman 480 metre gitmiş, bu durumda Selman 720 metre gidene kadar Alp 540 metre gider” gibi doğrudan orantıya gidip hatalı sonuç çıkarabilir. Oysa burada gözden kaçırılmaması gereken, 720 metreye ulaşmak için Selman’ın “ekstra” mesafe olarak 240 metre daha koşacağı, zamanın da o oranda artacağı ve Alp’in de bu süre zarfında mesafe kat edeceğidir. Dolayısıyla doğrudan 300:480 = x:720 gibi bir orantı kurmak hatalıdır. Doğru yol, hızlar üzerinden süreyi bulmaktır. -
Cevap Seçenekleri:
Problemin orijinalinde yer alan seçenekler (A) 360, (B) 270, (C) 240, (D) 180 idi. Yaptığımız hesaplama sonucu 270 metre elde edildi. Bu nedenle doğru seçeneğin (B) 270 olduğu görülür.
Sık Yapılan Hatalar ve Dikkat Edilmesi Gerekenler
-
Hızla Mesafeyi Karıştırma
Öğrencilerin en sık yaptığı hata, “hız” ile “mesafe” arasındaki farkı net ayırmadan orantı kurmaktır. Oysa hız sabit olsa bile, kat edilen mesafe zamanın çarpımıyla değişir. -
Oranı Tüm Problem İçin Yanlış Kullanma
Bir anda gözlenen oranı (örneğin Alp 300 m, Selman 480 m), finalde de doğrudan mesafe olarak orantılamaya kalkmak hatalıdır. İlk t zaman kuvvetli bir ipucudur ama asıl aranan final durumu, zamanla ilişkisi yeniden değerlendirilerek orantılanmalıdır. -
Birimleri Es Geçme
Soruda zaman birimi ifade edilmemiş olsa bile, “birim zaman” olarak ne kullanıldığı önemli değildir.- Eğer metre / saniye olarak alırsak, v_A = 300 / t (m/s).
- Eğer metre / dakika olarak alırsak, v_A = 300 / t (m/dk).
Sonuç aynı orana bağlıdır. Yeter ki tutarlı olalım.
-
Toplam Pist Uzunluğunu Yanlış Kabul Etme
Soruyu hızlı okuyan bazı öğrenciler, pist toplam uzunluğunun 720 değil 540 metre zannedebiliyor (örneğin Selman’ın koştuğu 480 m ile Alp’in 300 m’sini yanlış toplayarak). Oysa soruya göre pistin tamamı 720 metredir. Bunları karıştırmamak gerekir.
Özet Tablo
Aşağıdaki tablo, sorunun temel verilmesini, hız oranını ve nihai sonucun hesaplanmasını kısaca özetler:
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Başlangıç Verileri | - Pist uzunluğu: 720 m - Zaman t sonundaki konumlar: Alp: 300 m Selman: 720 - 240 = 480 m |
|
| 2. Hız Oranı | v_A = 300/t, v_S = 480/t \Rightarrow v_S / v_A = \frac{480/t}{300/t} = \frac{480}{300} = \frac{8}{5} |
Selman’ın hızı : Alp’in hızı = 8 : 5 |
| 3. Selman’ın 720 m Koşması İçin Süre | 720 = v_S \times T = \left(\frac{480}{t}\right) \times T \Rightarrow T = \frac{720 \cdot t}{480} = 1.5 \, t |
Selman bitişe vardığında zaman T = 1.5 t |
| 4. Aynı Sürede Alp’in Aldığı Yol | v_A \times T = \left(\frac{300}{t}\right) \times (1.5\, t) = 450 m | Alp 450 m koşmuştur |
| 5. Bitime Kalan Mesafe (Alp için) | 720 - 450 = 270 m | Cevap: 270 m |
Sonuç ve Kısa Özet
- İki koşucunun sabit hızlar ile koştuğu durumlarda, bir andaki mesafelerinin oranı bize hız oranlarını verir.
- Buna göre, sorudaki gibi, Alp 300 m, Selman 480 m kat etmişse, Selman’ın hızı Alp’in hızının \frac{8}{5} katıdır.
- Selman 720 metreye ulaştığında (bitiş çizgisi), Alp ise 450 metreye ulaşır.
- Alp’in bitiş çizgisine kalan mesafesi bu anda:720 - 450 = 270 \text{ metredir.}
Doğru cevap: 270 metre (genellikle testlerdeki “B) 270” seçeneği).
Kısa Özet: Bu tip bir sabit hız probleminde, koşucuların aynı anda başladığı zamandaki mesafe oranını bulmak, en kolay yoldan hız oranını verir. Sonraki durumlar (örneğin birinin bitiş çizgisine ulaştığı an) hesaplanırken bu hız oranları kullanılarak zaman oranı üzerinden sonuca gidilir.
Kaynaklar
- MEB 7. Sınıf Matematik Ders Kitabı (Güncel müfredat)
- Ortaokul Matematik Hareket ve Hız Problemleri Etkinlikleri
- Çeşitli çevrimiçi soru bankaları ve örnek testler