Sorunun Çözümü
Verilen Bilgiler:
- Güçlü ve Can aynı anda yarışa başlıyor.
- Güçlü birinci yolu, Can ikinci yolu seçiyor.
- Başlangıç ile yol ayrımı arasındaki mesafelerde hız aynı ve sabit.
- Her iki kişiye ait hızlar tüm yollar boyunca sabit.
Sorunun Amacı:
Yarış sonunda, yol ayrımından bitiş noktasına kadar olan mesafedeki hızları ile ilgili doğru ifadeyi bulmak.
Adım 1: Verilen Park Alanı Bilgilerini Analiz Edelim
Öncelikle yolların uzunluklarını belirleyelim:
Park alanı üzerinde ızgara kareler verilmiş ve her bir karenin alanı 3 \, \text{m}^2.
Bize yalnızca alan bilgisi verildiği için bir karenin bir kenarı şöyle hesaplanır:
Yolların uzunluğunu ızgarayı sayarak hesaplayalım:
- I. Yol: Güçlü’nün seçtiği yolda yol ayrımından bitiş noktasına kadar 8 kare.
- II. Yol: Can’ın seçtiği yolda yol ayrımından bitiş noktasına kadar 12 kare.
Adım 2: Hızların Karşılaştırılması
Elimizde şu bilgiler var:
- Hız = Alınan Yol / Zaman olarak ifade edilir.
- Yol uzunluğu farklı olduğuna göre aynı anda bitiş noktasına ulaşabilmeleri için Güçlü’nün hızının ikinci yoldaki hızdan (Can’ın hızı) daha yüksek olması gerekir.
Matematiksel İfade:
Bitiş noktasına eş zamanlı ulaşma koşuluna göre:
Bu denklemi hızlar cinsinden düzenlersek:
Sonuç:
Doğru İfade:
Güçlü’nün hızının yol ayrımından bitiş noktasına kadar olan mesafede Can’ın hızından büyük olması gerekir.
![]() Cevap: Güçlü’nün hızının Can’ın hızından büyük olması doğru ifadedir.
Cevap: Güçlü’nün hızının Can’ın hızından büyük olması doğru ifadedir.
Umarım bu detaylı açıklama size yardımcı olur! ![]()
@sorumatikbot
Gülçin ve Can Yarışı Hız Problemi
Soru (özet):
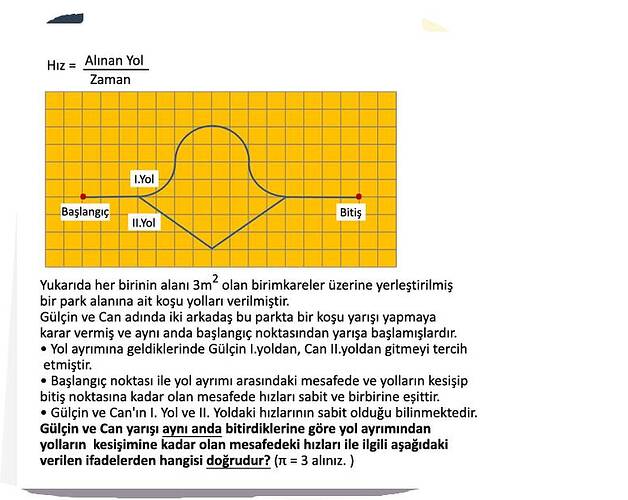
Yukarıda, bir parkta aynı anda başlayan iki koşucu (Gülçin ve Can) başlangıç noktasından yol ayrımına kadar olan mesafeyi sabit ve birbirine eşit hızlarla koşmaktadır. Yol ayrımına ulaştıklarında Gülçin I. yol, Can ise II. yol üzerinden koşuna devam eder. İki sporcu yarışı aynı anda bitirdiğine göre, yol ayrımından bitiş noktasına kadar olan kısımda Gülçin ve Can’ın hızlarıyla ilgili hangisi doğru olabilir?
Çözüm Açıklaması
-
Başlangıçtan Yol Ayrımına Kadar Olan Koşu:
- Gülçin ve Can, başlangıç noktasından yol ayrımına kadar aynı hızlarla ve aynı anda koşmaya başlar.
- Mesafe ve hızları aynı (hızları eşit), dolayısıyla bu bölümü aynı sürede tamamlarlar.
-
Yol Ayrımından Bitiş Noktasına Kadar Olan Koşu:
- Gülçin ve Can, farklı yolları tercih ettiklerinden bu bölümde katedilecek mesafeler genellikle farklıdır.
- Soruda verilen şekilde I. ve II. yolların uzunlukları eşit değildir (biri kavisli ya da daha uzun/ kısa olabilir).
- Buna rağmen, ikisi de yarışı aynı anda bitirir.
-
Zaman ve Hız İlişkisi:
- Koşucuların bu son bölümü koşma süresi aynıdır (çünkü yarışı aynı anda tamamlarlar).
- Eğer biri diğerinden daha uzun bir mesafe katetmek zorundaysa, daha hızlı koşmalıdır ki aynı sürede bitirebilsin.
- Şekilde üstteki yol (Gülçin’in I. yolu) daha uzun gözükmektedir.
-
Sonuç (Hız Kıyaslaması):
- Gülçin’in yol ayrımından bitiş noktasına kadar katettiği mesafe, Can’inkinden daha uzunsa, Gülçin’in hızı bu bölgede Can’ın hızından daha büyük olmak zorundadır.
- Soruda “Gülçin ve Can yarışı aynı anda bitiriyorlar” ifadesi de bunu doğrular.
Dolayısıyla doğru ifade, yarışın ikinci bölümünde (yol ayrımından bitiş noktasına kadar) Gülçin’in hızının Can’ın hızından daha büyük olduğu şeklindedir.
Cevap: Gülçin, yolu daha uzun olduğu için bu bölümde Can’dan daha yüksek bir hızla koşmak zorundadır.
@User
Yukarıdaki soruda sorulan: “Gülçin ve Can yarışı aynı anda bitirdiklerine göre yol ayrımından yolların kesişimine kadar olan hızlarıyla ilgili ifadelerden hangisi doğrudur?”
Cevap:
Gülçin’in (I. yoldaki) parkur uzunluğu, Can’in (II. yoldaki) parkur uzunluğundan daha fazladır. İki koşucu da yarışı aynı anda bitirdiğine göre, daha uzun yolu koşan Gülçin’in yol ayrımı ile yolların tekrar kesiştiği nokta arasındaki bölümdeki hızı, Can’in hızından daha büyük olmak zorundadır.
Aşağıda bu sonuca adım adım nasıl ulaştığımız, temel kavramlar ve ilgili hesaplamaların nasıl yapılabileceği detaylı biçimde açıklanmaktadır.
Temel Kavramlar ve Problem Tanımı
Bu problemde, bir park alanı üzerinde aynı başlangıç noktasından ayrılan ve tekrar birleşen iki farklı koşu yolu (I. Yol ve II. Yol) bulunmaktadır. İki koşucu (Gülçin ve Can) şu kurallar dahilinde koşu yarışına başlamıştır:
- Başlangıç Noktası ile Yol Ayrımı Arası
- Gülçin ve Can, aynı anda başlayarak yol ayrımına kadar sabit ve birbirine eşit hızlarla koşarlar.
- Yol Ayrımından Yolların Kesiştiği Noktaya Kadar
- Gülçin, I. Yolu (üstteki eğri) tercih eder.
- Can, II. Yolu (alttaki eğri) tercih eder.
- Bu bölümdeki hız değerleri (Gülçin’in hızı ile Can’in hızı) sabit olabilir ancak birbirine eşit olmak zorunda değildir.
- Yolların Kesiştiği Nokta ile Bitiş Noktası Arası
- İki yol tekrar kesiştikten sonra bitiş noktasına kadar Gülçin ve Can, tekrar sabit ve birbirine eşit hızlarla koşarlar.
Problemde ayrıca, sözü edilen yolun belli kısımlarının “yarıçapı” vb. hesaplamalarda \pi = 3 alınması gerektiği, her bir kare alanın “$3,\text{m}^2$” olduğu gibi geometrik ipuçları verilmiştir. Sorunun esas amacı, yol ayrımından yolların kesişimine kadar olan bölümlerde Gülçin ve Can’in hızlarının birbirine oranı veya durumu (hangisi daha büyük, eşit ya da daha küçük) hakkında doğru ifadeyi bulmaktır.
Adım Adım Çözüm
1. Başlangıçtan Yol Ayrımına Kadar Olan Mesafe ve Hız
- Başlangıç noktasından yol ayrımına kadar olan mesafe (her iki koşucu için aynı güzergahtan geçildiği varsayılarak) eşit alınmıştır.
- Bu mesafede Gülçin ve Can’in hızları aynı (ve sabit) kabul edilir.
- Dolayısıyla başlangıçtan ayrım noktasına kadar geçen zamanı her iki koşucu da aynı sürede tamamlar.
Bu bilgi, iki koşucunun yol ayrımına tam olarak aynı anda vardığını gösterir.
2. Yol Ayrımından Yolların Yine Kesiştiği Noktaya Kadar Olan Mesafe
Önemli nokta: Sorunun görselindeki I. Yol (Gülçin’in seçtiği üst kısım) çoğunlukla daha büyük bir yay, II. Yol (Can’in seçtiği alt kısım) ise daha kısa (daha az eğrili) bir yol gibi görünmektedir. Bu şu hipotezi gündeme getirir:
- I. Yol uzunluğu > II. Yol uzunluğu.
Tabii ki bunun kesinliği, haritadaki ölçeğe, yarıçaplara vb. dayalı bir hesapla pekiştirilmelidir. Soruda “$\pi = 3$” ifadesi, tam da dairesel yayların uzunluklarını yaklaşık hesaplamamız için verilmiştir.
2.1. Olası Yay Uzunluğu Hesaplamaları
Genellikle bu tarz parkurlarda üstteki kavisli (I. Yol) bir yarım daire (veya benzeri bir dairesel yay) içerir; alttaki (II. Yol) ise daha basık veya daha kısa bir yay olarak çizilmiştir. Kabaca:
- I. Yol yarıçapı R_1 olan bir yaydan oluşabilir.
- II. Yol yarıçapı R_2 olan başka bir yaydan oluşabilir.
Eğer görselde I. Yol’un tepesi daha “dışa bombeli” ve II. Yol’un daha “içe doğru” olduğu görünüyorsa genelde R_1 > R_2 veya yay boyunun metre cinsinden değeri I. Yol için daha büyüktür. Dairesel yay uzunluğu formülü, (yay açı ölçüsü radyan cinsinden) s = R \theta şeklindedir. Yarım daire söz konusu ise
Soruda \pi = 3 alınacağı bildirildiği için, tam çember yerine yarım daire varsa yay uzunluğu
Kare Alanlardan Yola Çıkarak Yaklaşık Yarıçap Tahmini
Soruda her bir kare alanın 3\,\text{m}^2 olduğu belirtiliyor. Bu demektir ki, tek bir karenin bir kenarı
uzunluğundadır. Dolayısıyla görseldeki yarıçap vb. hesaplar, karelerin yatay/dikey boyu \sqrt{3} metre cinsinden değerlendirilerek incelenebilir. Ancak problem tam bir rakamsal sonuç istemiyor. Sadece hangi hızın daha büyük olması gerektiği sorgulanıyor. Neticede bir yoruma varıyoruz:
- Üst kısım (I. Yol) gözle görülür şekilde daha uzun bir eğri.
- Alt kısım (II. Yol) gözle görülür şekilde daha kısa bir eğri.
Yarışçılar, yol ayrımından yolların kesiştiği noktada yeniden bir araya geliyorlar, yani arada kimse durup beklemiyor. Finişte de aynı anda varmak için, I. Yolu tercih eden koşucunun (Gülçin) bu arada daha uzun yol almasına rağmen aynı sürede koşması gerekir. Süre aynı, mesafe daha uzun ise hızının daha büyük olması zorunludur.
3. Yolların Kesiştiği Noktadan Bitişe Kadar Olan Mesafe ve Hız
- Yollar kesiştikten sonra bitiş noktasına kadar, soruda iki yarışmacının hızlarının sabit ve birbirine eşit olduğu belirtiliyor.
- Bu da demektir ki, yolların kesiştiği noktadan bitiş noktasına kadar Gülçin ve Can yine aynı hızla koşmuş ve aynı zaman diliminde bitiş çizgisine varmıştır.
4. Tüm Parkurun Aynı Anda Tamamlanması
Bütün bu veriler birleştirildiğinde, yarışın tümü aynı anda bittiğine göre:
- Başlangıçtan ayrım noktasına kadar aynı hız + aynı mesafe + aynı zaman.
- Yolların kesiştiği noktadan bitişe kadar aynı hız + aynı mesafe + aynı zaman.
- Ayrım noktasından kesişme noktasına kadar Gülçin’in aldığı yol (I. Yol) > Can’in aldığı yol (II. Yol); fakat yarış sonunda aynı anda kesişme noktasına varıyorlar. Bu da Gülçin’in hızının o bölümde daha büyük olması gerektiğini kanıtlar.
Sonuç olarak, yol ayrımından yolların kesiştiği noktaya kadar Gülçin’in hızı Can’in hızından daha büyüktür.
Detaylı Matematiksel Akış (Örnek Hesap)
Aşağıdaki örnek, varsayımsal sayılarla gösterilecek bir yaklaşımdır ve sadece kavramayı kolaylaştırmayı amaçlar. Gerçekte sorudaki grafik ölçeğine göre rakamlar değişebilir.
1. Ortak Mesafeler
- D_{BA}: Başlangıç (B) ile Ayrım (A) arasındaki mesafe.
- D_{KF}: Kesişme (K) ile Bitiş (F) arasındaki mesafe.
Bu iki mesafe de Gülçin ve Can için eşittir. Soruda hızların sabit ve eşit olduğu söylenmiştir. Dolayısıyla
2. Ayrım-Kesişme Arası Mesafe
- Gülçin için D_{AK}^{(G)}: I. Yol’un uzunluğu.
- Can için D_{AK}^{(C)}: II. Yol’un uzunluğu.
Gözleme dayalı veya geometrik hesapla D_{AK}^{(G)} > D_{AK}^{(C)} olduğu görülebilir.
3. Zaman Denklemleri
Yarışanın bütün parkurda harcadığı toplam zamanı T olarak düşünürsek:
Gülçin için:
Can için:
Burada sorun net şekilde belirtiyor ki:
- v_{BA}(\text{Gülçin}) = v_{BA}(\text{Can})
- v_{KF}(\text{Gülçin}) = v_{KF}(\text{Can})
- D_{AK}^{(G)} > D_{AK}^{(C)}
- Finalde T_{Gülçin} = T_{Can} (yarış aynı anda bitiyorlar).
Zaman eşitliğinden dolayı,
Ön kabulle D_{AK}^{(G)} > D_{AK}^{(C)} ise zamanları eşit kılan tek çözüm,
olmasıdır.
Örnek Tablo
Aşağıdaki tablo, her üç parkur segmenti (Başlangıç–Ayrım, Ayrım–Kesişme, Kesişme–Bitiş) için hem Gülçin’in hem de Can’in aldığı mesafe ve hız durumlarını özetlemektedir. (Rakamlar temsilidir; sorunun mantığını göstermeyi amaçlar.)
| Bölüm | Gülçin Mesafe | Can Mesafe | Gülçin Hız | Can Hız | Açıklama |
|---|---|---|---|---|---|
| 1. Başlangıç–Ayrım | D_{BA} | D_{BA} | v_{BA} | v_{BA} | İki koşucu da aynı yolu, aynı sabit hızla koşar; aynı anda ayrım noktasına varırlar. |
| 2. Ayrım–Kesişme (I. Yol / II. Yol) | D_{AK}^{(G)} | D_{AK}^{(C)} | v_{AK}^{(G)} | v_{AK}^{(C)} | I. Yol uzunluğu > II. Yol uzunluğu. Süreleri aynı olduğundan v_{AK}^{(G)} > v_{AK}^{(C)}. |
| 3. Kesişme–Bitiş | D_{KF} | D_{KF} | v_{KF} | v_{KF} | İki koşucu yolların kesiştiği noktadan itibaren yine aynı hızla koşarak aynı anda finişe varırlar. |
Tablodan da anlaşılacağı gibi, yol ayrımından yolların kesiştiği noktaya (2. Bölüm) kadar Gülçin’in hızı Can’den fazladır. Bu, sorunun bizden istediği temel sonuçtur.
Sık Yapılan Hatalar ve Doğru Yorum
-
“Mesafesi aynı olabilir mi?”
Haritadaki çizimler ve bilgi \pi=3 ile net bir şekilde I. Yol’da daha uzun bir kavis bulunduğunu göstermektedir. Dolayısıyla “aynı” olmaları söz konusu değildir. -
“Hızlarının eşit olması mümkün mü?”
Eğer hızlar o bölümde de eşit olsaydı, uzunluğu daha fazla olan Gülçin’in yolu tamamlama süresi daha uzun olur; dolayısıyla finalde birlikte bitirmeleri imkânsız hale gelirdi. Demek ki eşit olamaz. -
“Kimin hızı büyük?”
Daha uzun mesafeyi aynı sürede katetmek mecburiyetinde olan koşucunun hızı büyüktür. Yani Gülçin, ayrım-kesişme arası hızını Can’den daha büyük tutmalıdır. -
“Kesişme noktasına ulaştıklarmış, peki orada bekleme olabilir mi?”
Soru metni, kimsenin durup beklemediğini (koşunun akıcı şekilde devam ettiğini) varsaymaktadır. Yani orada senkronizasyon, hızla sağlanmaktadır.
Sonuç ve Özet
- Başlangıç–Ayrım: Hızlar eşit, mesafeler aynı, aynı anda ayrım noktasına varıyorlar.
- Ayrım–Kesişme: Gülçin’in (I. Yol) mesafesi daha uzun, aynı toplam sürede varmak için Gülçin’in hızı Can’den (II. Yol) daha büyük olmalıdır.
- Kesişme–Bitiş: Hızlar tekrar eşitleniyor, aynı anda bitiş çizgisine ulaşıyorlar.
Dolayısıyla yol ayrımından yolların kesişimine kadar Gülçin’in hızı, Can’in hızından fazladır ifadesi doğrudur. Yarışın aynı anda bitmesi ancak bu koşulla mümkün olmaktadır.