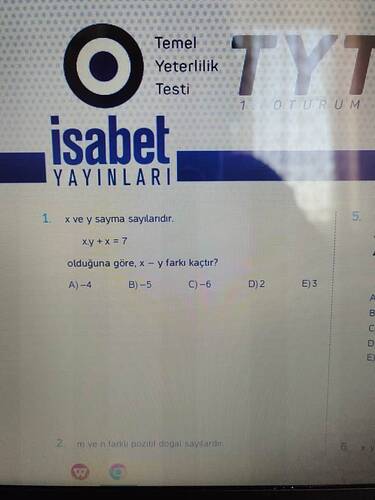
x ve y sayma sayılarıdır. x*y + x = 7 olduğuna göre, x - y farkı kaçtır?
Cevap:
Bu soruyu çözmek için şu adımları izleyelim:
-
Denklemi sadeleştirin:
$$ x \cdot y + x = 7 $$Denklemi sadeleştirebiliriz, her iki tarafı da x ile bölerek:
$$ x(y + 1) = 7 $$ -
Sayma sayıları olan x ve y’yi belirleyin:
x ve y sayma sayılarıdır (pozitif tam sayılar). 7 bölünebilen sayma sayı kombinasyonlarını kontrol edelim.$$ x(y + 1) = 7 $$
7, asal bir sayı olduğundan, sadece (1,7) veya (7,1) şeklinde çarpanlara ayrılabilir. Dolayısıyla, x ve y + 1 de bu çarpanlar olabilir.
-
x = 1 için:
$$ 1 \cdot (y + 1) = 7 $$
$$ y + 1 = 7 $$
$$ y = 6 $$ -
x = 7 için:
$$ 7 \cdot (y + 1) = 7 $$
$$ y + 1 = 1 $$
$$ y = 0 $$
Ancak y = 0 bir sayma sayısı değildir. Bu yüzden bu çözüm geçersizdir.
-
-
Farkı hesaplayın:
Geçerli tek çözüm x = 1 ve y = 6 olduğundan,
$$ x - y = 1 - 6 $$
$$ x - y = -5 $$
Sonuç:
x - y farkı -5’tir. Doğru cevap: B) -5