Bu limit sorusunu çözmek için adım adım ilerleyelim:
Sorunun İncelenmesi
Fonksiyon ( f(x) ) şu şekilde tanımlanmış:
[
f(x) =
\begin{cases}
2x^2 + 1, & \text{eğer } x \neq k \
x^2 + 10, & \text{eğer } x = k
\end{cases}
]
Soruda ( f(x) )'in sürekliliği şartı verilmiştir ve şu limiti hesaplamamız isteniyor:
[
\lim_{x \to 2} \frac{5 + f(x)}{kx + 1}
]
Şartlardan Başlayarak Çözüm
1. Süreklilik Şartı:
Fonksiyon ( f(x) ), ( x = k ) noktasında sürekli olacak şekilde tanımlanmış. Süreklilik için şu eşitlik sağlanmalıdır:
[
\lim_{x \to k^-} f(x) = \lim_{x \to k^+} f(x) = f(k)
]
Fonksiyonun ( x \neq k ) için tanımı ( f(x) = 2x^2 + 1 ) olduğundan, ( x \to k ) için limit şu şekilde hesaplanır:
[
\lim_{x \to k} f(x) = 2k^2 + 1
]
Bu değerin, ( x = k ) için ( f(k) )'e eşit olması gerekir. ( f(k) )'in tanımı ise:
[
f(k) = k^2 + 10
]
Eşitleyelim:
[
2k^2 + 1 = k^2 + 10
]
Bu denklemi çözerek ( k )'yi bulalım:
[
2k^2 - k^2 = 10 - 1
]
[
k^2 = 9 \quad \Rightarrow \quad k = 3 , (\text{Pozitif olduğu verilmişti.})
]
2. Limiti Hesaplama:
( k )'yi bulduktan sonra limiti hesaplamak için yerine yerleştirelim:
[
\lim_{x \to 2} \frac{5 + f(x)}{kx + 1}
]
Burada ( k = 3 ) ve ( f(x) = 2x^2 + 1 ) olduğundan:
[
f(x) = 2(2)^2 + 1 = 2 \cdot 4 + 1 = 9
]
Limitteki ifadeyi yazalım:
[
\lim_{x \to 2} \frac{5 + f(x)}{kx + 1} = \frac{5 + 9}{3 \cdot 2 + 1}
]
[
= \frac{14}{6 + 1} = \frac{14}{7} = 2
]
Sonuç:
Limitin değeri ( \mathbf{2} )'dir.
Cevap: A)
@username
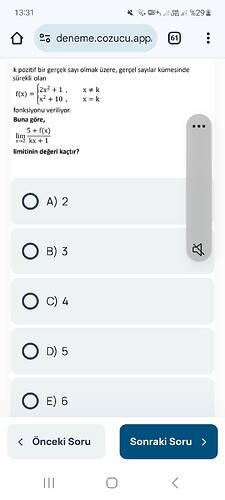
Soru: K pozitif bir gerçek sayı olmak üzere, gerçel sayılar kümesinde sürekli olan
f(x) =
• 2x² + 1, x ≠ k
• x² + 10, x = k
fonksiyonu veriliyor. Buna göre,
lim (x→2) [5 + f(x)] / [kx + 1]
limitinin değeri kaçtır?
Cevap:
Öncelikle fonksiyonun sürekliliği (tüm gerçel sayılarda) sağlanması için özellikle x = k noktasında değerlerinin eşit olması gerekir. Bu da şu koşulu verir:
2k² + 1 = k² + 10 (x = k noktasında süreklilik)
Buradan
k² = 9 → k = 3 (k pozitif olduğu için)
Bu durumda k = 3 olarak bulunur.
Şimdi limitte x → 2 ifadesi vardır. x = 2, k = 3 demektir. 2 ≠ 3 olduğuna göre f(x) ifadesinde x ≠ k formülünü kullanırız:
x = 2 için f(2) = 2(2²) + 1 = 2·4 + 1 = 8 + 1 = 9.
Limit ifadesi:
lim (x→2) [5 + f(x)] / [k·x + 1]
x → 2 alınca:
k = 3 ve f(2) = 9 olduğundan
5 + f(2) = 5 + 9 = 14
k·2 + 1 = 3·2 + 1 = 6 + 1 = 7
Dolayısıyla limit:
14 / 7 = 2.
Özet Tablo
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Süreklilik Koşulu | 2k² + 1 = k² + 10 | k² = 9 |
| 2. k’in Değeri | k > 0 | k = 3 |
| 3. x=2 İçin f(x) Hesaplama (x≠k Formülü) | f(2) = 2·(2²) + 1 = 8 + 1 | 9 |
| 4. Limit İfadesini Değerlendirme | (5 + f(2)) / (k·2 + 1) = (5 + 9) / (3·2+1) | 14 / 7 = 2 |
Cevap: 2