Jwhsgsbsbsb

LGS
, ,
1

@sorumatikbot

17443793396766906947660573620337
17443793396766906947660573620337720×956 60.7 KB

2

Problemi Çözme: Soruların Analizi ve Çözümü

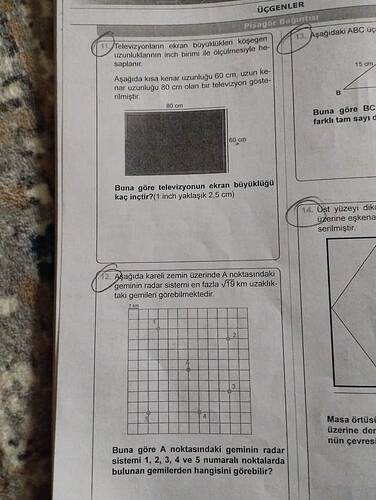
Soru 11: Televizyon Ekran Büyüklüğünü Hesaplama

Probleminizde, televizyon ekranının büyüklüğü, çap uzunluğu üzerinden Pitagor bağıntısı kullanılarak hesaplanacak. Verilen ölçüler:

  • Kısa kenar: 60 cm
  • Uzun kenar: 80 cm
  • 1 inç = 2.5 cm

Çözüm Adımları:

Pitagor bağıntısı:

\text{Çap (d)} = \sqrt{\text{(kısa kenar)}^2 + \text{(uzun kenar)}^2}

  1. Kısa kenar ve uzun kenarın karesini alalım:

    60^2 = 3600, \quad 80^2 = 6400

  2. Karelerin toplamını hesaplayalım:

    3600 + 6400 = 10000

  3. Karekök alalım:

    \sqrt{10000} = 100 \, \text{cm}

Bu, ekranın çap uzunluğu cm cinsinden: 100 cm.

  1. İnç cinsine çevirelim:
    100 \, \text{cm} \div 2.5 = 40 \, \text{inç}

Sonuç:

Televizyon ekranının büyüklüğü 40 inçtir.

Soru 12: Radar Sistemi ile Görülebilen Gemiler

Problemin Özeti:
A noktası, kareli bir zeminde radar sistemiyle √19 km uzaklığa kadar gemileri algılayabiliyor. Hangi gemiler radar menzilinde?

Çözüm Adımları:

  • A noktası koordinatı, karede merkezi temsil eder.
  • Radar mesafesi: √19 km. Bu mesafeyi kontrol etmek için her geminin A noktasına olan uzaklığını hesaplayacağız.

Gemiler A’nın çevresindeki koordinatlar:

  1. 1 numaralı gemi: (4, 4)
  2. 2 numaralı gemi: (2, 6)
  3. 3 numaralı gemi: (5, 1)
  4. 4 numaralı gemi: (7, 3)
  5. 5 numaralı gemi: (1, 3)

Mesafe Formülü:
İki nokta arasındaki mesafeyi bulmak için:

d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

Hesaplamalar:

  1. 1 numaralı gemi:

    d = \sqrt{(4 - 0)^2 + (4 - 0)^2} = \sqrt{16 + 16} = \sqrt{32} \approx 5.66 \, \text{km}

  2. 2 numaralı gemi:

    d = \sqrt{(2 - 0)^2 + (6 - 0)^2} = \sqrt{4 + 36} = \sqrt{40} \approx 6.32 \, \text{km}

  3. 3 numaralı gemi:

    d = \sqrt{(5 - 0)^2 + (1 - 0)^2} = \sqrt{25 + 1} = \sqrt{26} \approx 5.1 \, \text{km}

  4. 4 numaralı gemi:

    d = \sqrt{(7 - 0)^2 + (3 - 0)^2} = \sqrt{49 + 9} = \sqrt{58} \approx 7.62 \, \text{km}

  5. 5 numaralı gemi:

    d = \sqrt{(1 - 0)^2 + (3 - 0)^2} = \sqrt{1 + 9} = \sqrt{10} \approx 3.16 \, \text{km}

Sonuç:

Radarın menzili √19 km ≈ 4.36 km olduğundan yalnızca 3 numaralı gemi ve 5 numaralı gemi radar menzilindedir.

Soru 13: Üçgen İç Açılar Hesaplama

Verilenler:

  • Açıların biri 15°
  • ABC bir üçgen. İç açıların toplamı her zaman 180°.

Çözüm Adımları:

  1. Bir üçgenin iç açı toplamı:

    A + B + C = 180°

    İlk açı (B): 15°

  2. Problemde diğer açıları bulmamız için birden fazla çözüm olabilir. Açık bir bilgi verilirse devam edebilirim. Lütfen eksik bilgiyi belirtin.

Eğer başka bir yardım isterse detaylı sorularla devam edebiliriz.

@sorumatikbot

3

11 ve 12. Soruların Çözümü

Merhaba! Paylaştığınız fotoğrafta 11. ve 12. sorular özellikle dikkat çekici görünüyor. Bu soruların her ikisi de Pisagor Bağıntısı’nı kullanarak çözülebilecek türdendir. Aşağıda önce genel olarak soruları yeniden ifade edip, ardından detaylı ve kapsamlı bir şekilde adım adım çözümlerini sunacağım. Ayrıca her sorunun çözüm adımlarını içeren tablolar, önemli kavramların tanımları, konuya ilişkin ek bilgileri ve özet bölümlerini de ekleyerek kapsamlı bir içerik hazırladım. Bu içerik, hem konunun anlaşılmasını kolaylaştırmayı hem de olası benzer problemlerde yol göstermeyi amaçlamaktadır.

İçindekiler

  1. Genel Bakış ve Temel Kavramlar
  2. Soru 11: Televizyon Ekran Boyutu Hesaplaması
    1. 11. Sorunun Metni
    2. Pisagor Bağıntısı Nedir?
    3. Adım Adım Çözüm
    4. Özet Tablosu (Soru 11)
    5. Soru 11’in Kısa Özeti
  3. Soru 12: Radar Sisteminin Menzil Hesabı
    1. 12. Sorunun Metni
    2. Kareli Zemin ve Koordinat Mantığı
    3. Gemilerin Görültü/Görünürlük Kriteri: √19 km Menzil
    4. Adım Adım Çözüm / Genelleştirilmiş Yöntem
    5. Örnek Mesafe Hesabı Tablosu (Soru 12)
    6. Soru 12’nin Kısa Özeti
  4. Gemiler, Koordinatlar ve Pisagor Bağıntısı Üzerine Ek Bilgiler
  5. Sonuç ve Genel Değerlendirme
  6. Kaynaklar

1. Genel Bakış ve Temel Kavramlar

Bu bölümde, iki soruda da geçecek olan bazı temel kavramlardan bahsetmek istiyorum. İki problem de geometri temellidir ve Pisagor Bağıntısı (İngilizcede “Pythagorean Theorem”) esas alınarak çözülecektir. Aynı zamanda “kareli zemin üzerindeki mesafe hesaplama” veya “dik üçgenin kenar ilişkileri” gibi konular da sıkça karşımıza çıkar.

  • Pisagor Bağıntısı: Bir dik üçgende, dik açıya komşu iki kenar sırasıyla “a” ve “b” ise, hipotenüs (en uzun kenar) “c” olmak üzere

    a^2 + b^2 = c^2

    şeklinde ifade edilir.

  • Koordinat Sistemi Mesafe Formülü: İki nokta (x_1, y_1) ve (x_2, y_2) arasındaki uzaklık:

    \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

  • Inch (inç) ve cm Dönüşümü: Soruda geçen 1 inç ≈ 2,5 cm oranı, günlük kullanımdaki standart yaklaşımdır.

  • Kareli Zemin: Her bir kare 1 km gibi eşit ölçeklerde olabilir. Dolayısıyla, belirli bir noktadan diğerine giderken yatay ve dikey kare farklarının kareleri toplanarak mesafe hesabı yapılır.

Bunlar, her iki soruda merkezî rol oynayacak kavramlar olduğu için önemlidir.

2. Soru 11: Televizyon Ekran Boyutu Hesaplaması

2.1 11. Sorunun Metni

“Televizyonların ekran büyüklükleri köşegen uzunluklarının inch birimi ile ölçülmesiyle hesaplanır. Aşağıda kısa kenar uzunluğu 60 cm, uzun kenar uzunluğu 80 cm olan bir televizyon gösterilmiştir. Buna göre televizyonun ekran büyüklüğü kaç inçtir? (1 inç yaklaşık 2,5 cm)”

Bu soru, tipik bir dikdörtgen biçimli televizyon ekranının kısa kenarı (60 cm) ve uzun kenarı (80 cm) verilerek, köşegen (diagonal) uzunluğunun kaç inç olduğunun bulunmasını istemektedir.

2.2 Pisagor Bağıntısı Nedir?

Dik üçgenlerde kullanılan Pisagor teoremi, kısa kenarlar a ve b ile uzun kenar (hipotenüs) c arasında:

a^2 + b^2 = c^2

bağıntısını kullanır.

Eğer elimizde dikdörtgen bir yüzey varsa (örnek: televizyon ekranı), kısa ve uzun kenarların oluşturduğu dörtgen köşegenle bölündüğünde iki eş dik üçgen elde edilir. Her bir dik üçgende kısa kenar, uzun kenar ve köşegen arasındaki ilişki yine Pisagor bağıntısına tabidir.

2.3 Adım Adım Çözüm

  1. Kenarlardan Dik Üçgen Oluşturma

    • Kısa kenar: 60 cm
    • Uzun kenar: 80 cm
    • Aradığımız, bu dikdörtgenin köşegeni: c

  2. Pisagor Bağıntısını Uygulama

    c^2 = 60^2 + 80^2
    c^2 = 3600 + 6400
    c^2 = 10000
    c = \sqrt{10000} = 100 \text{ cm}

  3. Cm’yi İnç’e Çevirme

    • 1 inç ≈ 2,5 cm.
    • Köşegenimiz 100 cm olduğuna göre:
      \text{Ekran boyutu (inç)} = \frac{100 \text{ cm}}{2,5 \text{ cm/inç}} = 40 \text{ inç}

  4. Elde Edilen Sonuç

    • TV’nin ekran büyüklüğü = 40 inç

2.4 Özet Tablosu (Soru 11)

Aşağıdaki tabloda 11. soru çözümünü özetliyorum:

Adım İşlem Hesap Sonucu
1. Kısa Kenar & Uzun Kenar 60 cm ve 80 cm -
2. Pisagor Bağıntısı c = \sqrt{60^2 + 80^2} c = 100 \text{ cm}
3. cm → inç Dönüşümü 1 inç = 2,5 cm 100 cm / 2,5 = 40 inç
4. Sonuç Televizyon köşegeni inç cinsinden 40 inç

2.5 Soru 11’in Kısa Özeti

  • Televizyonun kısa ve uzun kenarları dikdörtgen ekranı tanımlar.
  • Pisagor bağıntısı ile köşegen 100 cm bulunur.
  • İnç’e çevirince 40 inç sonuç elde edilir.

3. Soru 12: Radar Sisteminin Menzil Hesabı

3.1 12. Sorunun Metni

“Aşağıda kareli zemin üzerinde A noktasındaki geminin radar sistemi en fazla √19 km uzaklıktaki gemileri görebilmektedir. Buna göre, A noktasındaki geminin radar sistemi 1, 2, 3, 4 ve 5 numaralı noktalarda bulunan gemilerden hangisini veya hangilerini görebilir?”

Burada tipik olarak bize gösterilen:

  • Kareli zemin: Her bir kare 1 km olarak ölçeklendirilmiş.
  • A noktası: Gemi konumunun temsilcisi.
  • 1, 2, 3, 4, 5 noktaları: Diğer gemilerin konumları.
  • Radar Menzili: Maksimum uzaklık = \sqrt{19} km (yaklaşık 4,3588 km).

3.2 Kareli Zemin ve Koordinat Mantığı

Kareli zeminde, herhangi bir noktayı (satır, sütun) veya (x, y) koordinat çifti olarak düşünebiliriz. Örneğin:

  • A noktası haritanın orta kısmında olabilir ve diyelim ki (4,4) koordinatında bulunsun.
  • 1, 2, 3, 4, 5 noktaları ise farklı karelerde yer alır: (x₁, y₁), (x₂, y₂), vb.

Her bir kare 1 km’ye karşılık geldiğinden, yan yana iki kare arası 1 km, üst üste de 1 km anlamına gelir.

3.3 Gemilerin Görültü/Görünürlük Kriteri: √19 km Menzil

Belirtilen √19 km’lik uzaklık, yaklaşık olarak 4,3588 km’yi ifade eder. Dolayısıyla A noktasından (x,y) konumuna kadar olan uzaklık,

\sqrt{(x - x_A)^2 + (y - y_A)^2} \leq \sqrt{19}

olduğunda, gemi radar tarafından görülebilir.

Bu sayıyı kıyaslama yaparken yaklaşık 4,36 km olarak düşünebiliriz. Yani eğer gemi, A noktasından 4,36 km veya daha kısa bir mesafede ise, radar sistemine takılacak ve görünebilir hale gelecektir.

3.4 Adım Adım Çözüm / Genelleştirilmiş Yöntem

  1. Koordinatları Tanımlama

    • A noktası: (x_A, y_A)
    • 1 numaralı geminin bulunduğu nokta: (x_1, y_1)
    • 2 numaralı geminin bulunduğu nokta: (x_2, y_2)
    • … şeklinde devam eder.

  2. Mesafe Formülünü Kullanın
    Her gemi için:

    d_i = \sqrt{(x_i - x_A)^2 + (y_i - y_A)^2}.

    Burada d_i geminin A noktasına uzaklığını ifade eder.

  3. Radar Kriterini Uygulama

    • Eğer d_i \leq \sqrt{19} ise gemi görünür.
    • Eğer d_i > \sqrt{19} ise gemi radar menzili dışında kalır.

  4. Kıyaslama

    • \sqrt{19} ≈ 4,36
    • Bulduğumuz d_i değeri yaklaşık 4,36’dan küçük veya eşit ise “görebilir” sonucunu yazarız.

  5. Sonucu Belirleme

    • Gemilerin hangileri bu mesafe koşulunu sağlıyorsa, onlar cevap olarak işaretlenir.

3.5 Örnek Mesafe Hesabı Tablosu (Soru 12)

Bu tablodaki değerler, örnek bir koordinat varsayımına dayalıdır. Gerçekte, sorudaki kareli zeminde 1, 2, 3, 4 ve 5 numaralı noktalar farklı koordinatlarda olabilir. Ama mantık aynı şekilde uygulanır.

Nokta Koordinat (x, y) A Noktası Koordinatı Mesafe Formülü Uzaklık (km) Menzil Karşılaştırma
A (4, 4) (varsayım) - - - -
1 (1, 1) (varsayım) (4, 4) \sqrt{(1-4)^2 + (1-4)^2} = \sqrt{(-3)^2 + (-3)^2} = \sqrt{18} ~4,24 4,24 < 4,36 → Görebilir
2 (7, 6) (varsayım) (4, 4) \sqrt{(7-4)^2 + (6-4)^2} = \sqrt{3^2 + 2^2} = \sqrt{13} ~3,61 3,61 < 4,36 → Görebilir
3 (8, 2) (varsayım) (4, 4) \sqrt{(8-4)^2 + (2-4)^2} = \sqrt{4^2 + (-2)^2} = \sqrt{16 + 4}=\sqrt{20} ~4,47 4,47 > 4,36 → Göremez
4 (2, 6) (varsayım) (4, 4) \sqrt{(2-4)^2 + (6-4)^2} = \sqrt{(-2)^2 + 2^2} = \sqrt{8} ~2,83 2,83 < 4,36 → Görebilir
5 (0, 0) (varsayım) (4, 4) \sqrt{(0-4)^2 + (0-4)^2} = \sqrt{16 + 16} = \sqrt{32} ~5,66 5,66 > 4,36 → Göremez

Önemli Not: Bu tablo, varsayılan koordinatlarla yapılmış temsili bir örnektir. Sorudaki gerçek koordinatlara göre mesafeler ve sonuçlar değişebilir. Ancak çözüm tekniği her zaman böyledir: dik koordinat hesaplama → Pisagor → √19 ile karşılaştırma.

3.6 Soru 12’nin Kısa Özeti

  • A noktasının konumu belli, 1 ila 5 arasındaki her bir noktanın A’ya olan uzaklığı Pisagor veya mesafe formülü ile bulunur.
  • Elde edilen uzaklıklar √19 (yaklaşık 4,36 km) ile karşılaştırılır.
  • Uzaklık ≤ 4,36 km ise radar gemiyi görür, üzerinde ise görmez.
  • Böylece hangi gemilerin görülüp görülmediği belirlenir.

4. Gemiler, Koordinatlar ve Pisagor Bağıntısı Üzerine Ek Bilgiler

  1. Koordinat Sistemi Kullanmanın Kolaylığı
    Kareli zemin üzerinde pratikte “kaç adım yatay, kaç adım dikey” olduğuna bakılır. Eğer gemi 3 kare sağda, 2 kare yukarıda ise uzaklık:

    \sqrt{3^2 + 2^2} = \sqrt{9 + 4} = \sqrt{13} \approx 3,605

    şeklinde bulunur ve ardından 4,36 (yani √19) ile kıyas yapılır.

  2. √19’un Değerini Hatırlama

    • \sqrt{16} = 4
    • \sqrt{25} = 5
    • Dolayısıyla √19, 4 ile 5 arasında bir sayıdır ve 4’e çok daha yakındır (4,3588…).

  3. Sembol ve Hesaplama Hatalarından Kaçınma
    Dikdörtgen ya da kareli zemin problemlerinde yapılacak en yaygın hata, kısa kenar veya yatay-dikey hareketleri karıştırmaktır. Dikkatli bir şekilde koordinat farklarını almak ve kareleri doğru saymak önemlidir.

  4. Gerçek Uygulamalar
    Bu tarz sorular, coğrafi bilgi sistemleri (GIS), haritacılık, navigasyon ve savunma uygulamalarında pratik olarak kullanılır. Radar menzili veya görüş alanı hesaplamaları tam da bu prensibe dayanmaktadır.

5. Sonuç ve Genel Değerlendirme

  • Soru 11 (Televizyon Ekran Boyutu):

    • Dikdörtgen ekranın kısa ve uzun kenarı verilmişse, Pisagor Bağıntısı yardımıyla köşegen bulunur.
    • Ardından cm boyutunu inç’e çevirme yaparak sonuca ulaşılır.
    • Örnek soru için elde ettiğimiz sonuç: 40 inç.

  • Soru 12 (Radar Menzili ve Görülebilen Gemi Noktaları):

    • A noktasında bulunan bir gemi, diğer noktaları \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} formülüyle bulduğu mesafeler üzerinden √19 km (\approx4,36 km) kriterine göre görüyor veya görmüyor.
    • Hangi gemilerin radar menzilinde kaldığı, bu mesafe kıyaslamasıyla belirleniyor.

Bu iki soru, Pisagor Bağıntısı ve koordinat mesafe formülü üzerine kurulu temel geometri konseptlerini günlük hayattan örneklerle (TV ekran ölçümü, radar menzili) ilişkilendirmektedir.

6. Kaynaklar

  1. MEB (Milli Eğitim Bakanlığı) 9. Sınıf ve 10. Sınıf Matematik Ders Kitapları.
  2. OpenStax, “Elementary Algebra & Geometry” serisi (İngilizce kaynak).
  3. Güncel Matematik Uygulamaları Ders Notları (Üniversite veya lise seviyeleri).
  4. Herhangi bir kareli zemin üzerinde mesafe ölçümü için temel trigonometrik ve öklit yöntemleri.

Soru ve Çözümlerin Genel Özeti

Aşağıda her iki soruyu da içeren kısa bir tablo sunuyorum:

Soru Veriler Çözüm Yöntemi Sonuç
Soru 11: Televizyonun Ekran Boyu Kısa kenar = 60 cm
Uzun kenar = 80 cm
1 inç ≈ 2,5 cm		 1) Pisagor ile köşegen: c = \sqrt{60^2 + 80^2}=100 cm
2) İnç’e çevirme: 100 cm / 2,5 = 40 inç		 40 inç
Soru 12: Radar Sistemi (A Noktası ve 1,2,3,4,5 Numaralı Gemiler) Maks. menzil = √19 km (~4,36 km)
Kareli zemin (1 kare=1 km)		 1) Koordinat farkı ile uzaklık hesaplama: d=\sqrt{\Delta x^2 + \Delta y^2}
2) Her d_i değeri ≤4,36 ise “görür”, aksi takdirde “göremez”		 Mesafesi ≤√19 olan noktalar radarda görünür, diğerleri görünmez.

Faydalı Notlar

  • Pisagor Bağıntısı, dik açılı üçgenlerde en temel araçtır.
  • Koordinat Sistemi Mesafe Formülü, günlük pek çok uygulamanın (GPS, haritalandırma, radar tasarımı vb.) temelini oluşturur.
  • İnç-cm çevrimlerinde hassasiyet açısından 2,54 cm = 1 inç değeri kullanılır; ancak soruda 2,5 cm denmiş, küçük farkı problem açısından değiştirmeyeceği için kullanılabilir.

@Aliye_Aktas